Объяснение:
2.1 Отношение площадей подобных треугольников равно квадрату коэффициента подобия
S(CPK)/S(ABE)=k²
S(ABE)=S(CPK)/k²
A) S(ABE)=27/2²=6.75
Б) S(ABE)=27*3²/1=243
2.2 Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.
BC=1/2*EA=1/2*9=4.5
Зачем даны ET и EB я не знаю.
3.1 Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
Из этого выводится уравнением формула (по идее её должны проходить), которая принимает вид для этого тр-ка такой:
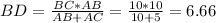
CD=10-6.66=3.33
ну там они в периоде после запятой.
Найдите углы ромба ABCD, если его диагонали AC И BD равны 4корень из 3 метров и 4 метра. (Для ясности нужно добавить фразу "О - точка пересечения диагоналей. ").
Решение: Пусть угол BAO=альфа. Диагонали ромба делят его углы ПОПОЛАМ, значит, угол DAO= углу BAO =альфа. Диагонали ромба взаимно ПЕРПЕНДИКУЛЯРНЫ, И ТОЧКОЙ ПЕРЕСЕЧЕНИЯ ДЕЛЯТСЯ ПОПОЛАМ, следовательно в прямоугольном треугольнике ABO катет AO равен 2*(корень из 3) метрАМ, а катет ВО равен 2 метрАМ. Поэтому тангенс альфа=1/(корень из 3), (Здесь нужно добавить, значит альфа равно 30 градусам) , а угол BAD=2*30= 60 градусам, угол ADC= (180 градусов минус угол ВАD)=120 градусам.
ответ 60 и 120 градусов (или Пи/3 и 2*Пи/3 радиан) .
Объяснение:
Двугранный угол при стороне пирамиды - это угол между высотой основания СН и апофемой (высотой грани) SH грани АSB по определению двугранного угла (так как СН и SH перпендикулярны ребру АВ). Прямоугольный треугольник SOH равнобедренный, так как его острый угол SHO=45°(дано). ОН=SO=5см. Но ОН=(1/3)*СН (поскольку треугольник АВС правильный), значит СН=15см, а ОС=ОВ=10см.
Тогда НВ=√(ОВ²-ОН²) или НВ=√(100-25)=5√3см, а АВ=2*НВ или АВ=10√3см. Боковое ребро пирамиды равно SB=√(ОВ²+SО²) или SB=√(100+25)=5√5см по Пифагору.
Тогда апофема SH=√(SВ²-HB²) или SН=√(125-75)=5√2см (по Пифагору).
Площадь боковой грани равна Sбг=(1/2)*АВ*SH или Sбг=(1/2)*10√3*5√2=25√6см².
Таких граней три, знаяит площадь боковой поверхности пирамиды равна Sб=75√6см².
Площадь основания - площадь правильного треугольника равна So=(√3/4)a² (a - сторона треугольника). So=(√3/4)300=75√3см².
Площадь полной поверхности пирамиды равна So+Sб=75√3+75√6=75√3(1+√2)см².
ответ: So=75√3см², Sб=75√6см², S=75√3(1+√2)см².