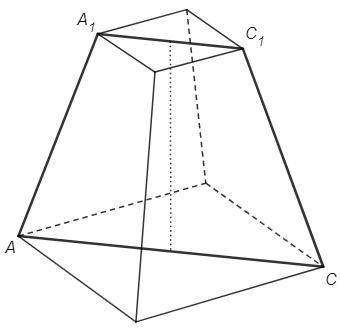
Правильная 4-я пирамида - в основании квадрат, боковые ребра равны. Пирамида усечена параллельно основанию. Диагональное сечение данной фигуры - равнобедренная трапеция.
Высота правильной пирамиды проецируется в центр описанной окружности основания. Центр описанной окружности квадрата - пересечение диагоналей. Диагональное сечение проходит через вершину и диагональ основания, следовательно высота лежит в плоскости сечения. Достаточно найти высоту сечения.
В сантиметрах
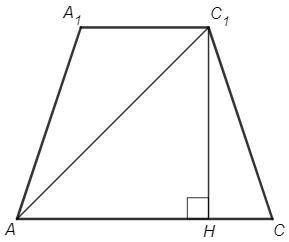
Рассмотрим трапецию AA1C1C.
A1C1 =A1B1 √2 =4√2 (диагональ квадрата)
AC =AB √2 = 8√2
Опустим высоту C1H.
AH =(AC +A1C1)/2 =6√2
C1H =√(AC1^2 -AH^2) =√(144-72) =6√2 (см)
S1 ≈ 19,8 cм².
S2 ≈ 3,9 cм².
Объяснение:
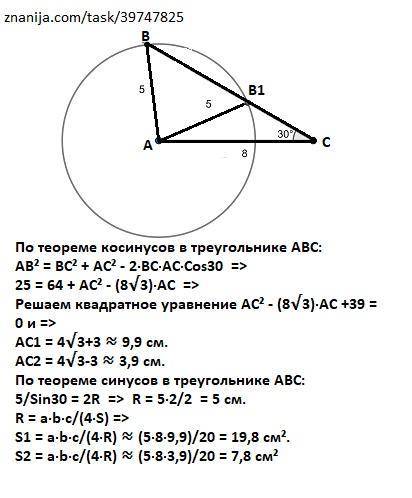
По теореме косинусов в треугольнике АВС:
АВ² = ВС² + АС² - 2·ВС·АС·Сos30 =>
25 = 64 + AC² - (8√3)·AC =>
Решаем квадратное уравнение AC² - (8√3)·AC +39 = 0 и =>
AC1 = 4√3+3 ≈ 9,9 см.
АС2 = 4√3-3 ≈ 3,9 см.
По теореме синусов в треугольнике АВС:
5/Sin30 = 2R => R = 5·2/2 = 5 см.
R = a·b·c/(4·S) =>
S1 = a·b·c/(4·R) ≈ (5·8·9,9)/20 = 19,8 cм².
S2 = a·b·c/(4·R) ≈ (5·8·3,9)/20 = 7,8 cм²
P.S. Для проверки на рисунке выполнено точное построение, доказывающее, что задача имеет два решения.