ответ: 32
Объяснение:
Противоположные углы равны, так что один угол 150, а второй 180-150 = 30 градусов.
Напротив угла 30 градусов лежит половина гипотенузы в прямоугольном треугольнике. Опустим высоту из точки B, например.
Получается бок сторона параллелограмма (8см) будет гипотенузой, а высота будет равна 8см / 2 = 4 см, т.к. напротив угла 30 градусов.
Можем найти второй катет по теореме Пифагора: x = 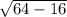 = 4
= 4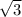 см
см
(но нам он не нужен)
Для нахождения площади параллелограмма нужно высоту умножить на бОльшую сторону)
8*4 = 32 см^2
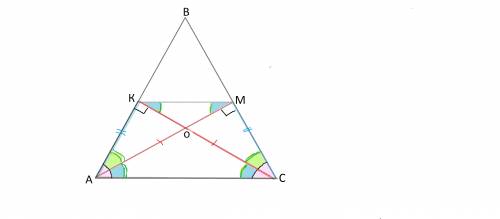
Рассмотрим треугольники АКС и СМА
Оба они - прямоугольные, имеют общую гипотенузу АС и равные острые углы:
∠А=∠С , т.к. треугольник АВС - равнобедренный и углы при основании АС равны.
Прямоугольные треугольники. в которых равны гипотенуза и острый угол - равны.
Из равенства этих треугольников следует, что
равны и треугольники АКМ и СКМ.
В этих треугольниках равны три стороны.
АМ=КС, АК=СМ, а КМ - общая.
Следовательно, углы КСМ=МАК
Но так как ∠А=∠С, то ∠ А - ∠МАК= ∠С- ∠КСМ.
Мы доказали равенсто углов КСА= МАС
Треугольники АОС и КОМ равнобедренные и подобны,
так как имеют равные стороны КО=ОМ, ОС=ОА, ∠ КОМ=∠АОС как вертикальные, и отсюда углы при основаниях этих треугольников равны ( 180 - ∠АОС):2.
Из подобия равнобедренных треугольников следует, что углы МКС=КСА и КМА=МАС.
Но эти углы - накрестлежащие при КМ и АС и секущих КС и МА.
Следовательно, КМ||АС, что и требовалось доказать.
Пусть квадрат СКМН вписан в треугольник АВС, причем точка М лежит на АВ.
Примем сторону квадрата равной х.
Тогда АК=12-х, ВН=10-х
Площадь ∆ АВС состоит из площади двух прямоугольных треугольников и площади квадрата.
S АВС=Ѕ АКМ+Ѕ МВН+Ѕ КМНС. ⇒
12•10=(12-х)•х+(10-х)•х+2х²⇒
120=22х⇒
————
Или:
Проведем биссектрису СМ .
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.
АМ:ВМ=АС:ВС=12/10=
Откуда АВ=11 частей, и СВ:х=АВ:АМ=11/6⇒
11х=60
———
Можно использовать также подобие треугольников АКМ и МНВ, из чего следует
АК:МН=КМ:ВН - ответ будет, естественно, тем же.