Вариант 1.
Так как <ABC = 45°, то: <A = 90-45 = 45°.
И так как острые углы друг другу равны, то прямоугольный треугольник — равнобёдренный, тоесть: BC = AC.
//Росстояние от точки A — до плоскости "α" — это и есть катет AC.//
У нас есть 2 условия: AB+BC = 17; AC-BC = 7.
И так как эти 2 катета равны — то составим систему только с одной переменной "x": 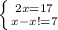
Э-э, стоп, что? Разность двух равных чисел не равна 7-и? Недопустимо!
Задача с ошибкой, если один и острых углов равен 45°, то второй тоже. Катеты равны, тоесть их разность не может быть равной 7-и.
Вариант 2.
Проигнорируем определение острого угла 45-градусов, представим, что нам известно только это: AC+BC = 17; AC-BC = 7.
Этой информации нам достаточно, чтобы найти катеты.
Но только на этот раз — переменных будет 2: AC = "x"; BC = "y".
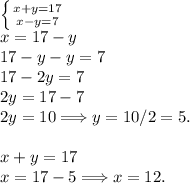
Вывод: AC = 12.
Пусть A' – середина дуги BC. Так как OA' || IA2, прямые OI и A'A2 пересекаются в точке K – центре гомотетии описанной и вписанной окружностей (см. рис.). Докажем, что K – искомый радикальный центр.
Первый Так как инверсия с центром A' и радиусом A'B меняет местами прямую BC и описанную окружность Ω треугольника ABC, точка A1 переходит в A, а A2 – в точку A'' пересечения прямой A'A2 с описанной окружностью. Следовательно, точки A, A1, A2 и A'' лежат на одной окружности.
Степень точки K относительно описанной окружности треугольника AA1A2 равна – KA2·KA'' = – r/R AA'·KA'' = r/R s(K), где s(K) – степень точки K относительно Ω.
Очевидно, степени точки K относительно описанных окружностей треугольников BB1B2 и CC1C2 будут такими же, то есть K – радикальный центр трёх окружностей.
Второй Пусть A', B', C' – середины дуг BC, CA, AB. Тогда треугольник A'B'C' переводится в A2B2C2 гомотетией с коэффициентом r/R и центром K, то есть KA2 : A'A2 = KB2 : B'B2 = KC2 : C'C2 = k : 1. Для точек прямой A'A2 разность степеней относительно описанной окружности треугольника AA1A2 и вписанной окружности треугольника ABC является линейной функцией. В точке A2 эта функция равна нулю,
а в точке A' – r², поскольку A'A1·A'A = A'B² = A'I² (первое равенсто следует из подобия треугольников A'A1B и A'BA, а второе – из леммы о трезубце – см. задачу 53119). Значит, в точке K эта разность равна – kr². Другие аналогичные разности в точке K также равны – kr², откуда и следует требуемое
По условию АВ⊥АD, ВС║AD, значит, АВ⊥ВС ⇒ трапеция АВСD - прямоугольная. Средняя линия МN=(ВС+AD):2 ⇒ BC+AD=2•MN=2•18=36. BC:AD=1:8, следовательно, AD=8BC и сумма оснований равна BC+8BC=9BC ⇒ BC=36:9=4. AD=8•4=32.
Сумма углов при одной стороне трапеции равна 180° (внутренние односторонние). Поэтому угол СDA=45°. Опустим из вершины С высоту СН. AH=BC=4. Отрезок НD=32-4=28. Треугольник СНD прямоугольный. Из суммы углов треугольника ∠DСH=180°-90°-45°=45° ⇒ ∆ СDH - равнобедренный. СН=НD=28. По построению СН⊥AD и АВ⊥AD по условию. Два перпендикуляра между параллельными сторонами равны. ⇒ АВ=СН=28 (ед. длины)