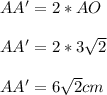
Объяснение:
1) Т.к. треугольники, образованные основаниями и отрезками диагоналей подобны, то ΔВОС~ΔАОD и :
ВО : ОD= ОС : ОА = ВС : АD, а так же как h₁ : h₂, где h₁ и h₂ - высоты соответствующих треугольников.
Кроме того,
SΔвос : SΔaod = ВС² : АD² → 4 : 16 = ВС² : АD², откуда
ВС = √4 =2см
АD = √16 = 4см
2) h₁ : h₂ = ВС : АD = 2/4 = 1/2
SΔвос = ½ ВС*h₁ = 4(см²), тогда
h₁ = 4*2/2 = 4(см)
SΔaod = ½АD*h₂ = 16(см²) , откуда
h₂ = 16*2/4 = 8(см)
h = h₁ + h₂ = 4 + 8 = 12(см)
3) Sавcd = (DC + AВ) * h /2 =(2+4)*12/2 = 36(см²) = площадь трапеции
4) Треугольники, образованные отрезками диагоналей и боковыми сторонами, равновелики, т.е.
SΔаов = SΔсоd = (Sавcd - SΔвос - SΔaod) / 2 =
= (36 - 4 - 16)/2 = 16/2 = 8 (см²)
Ребро октаэдра = 6 cm
Высота октаэдра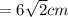 
Объяснение:
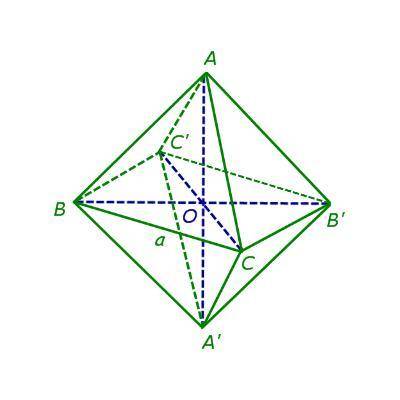
Предположим что речь идёт о правильном октаэдре. Тогда его грани - это восемь равносторонних треугольников (см. рисунок).
⇒ площадь одной грани (равностороннего треугольника)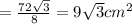 
Т.к. площадь одной грани это площадь равностороннего треугольника, углы которого равны между собой, и равны 60° ⇒ есть такая формула площади треугольника:
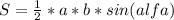- где a, b — стороны, alfa — угол между ними.
Т.к. наш треугольник равносторонний ⇒ a = b, a alfa = 60°, то подставив имеющиеся значения получим:
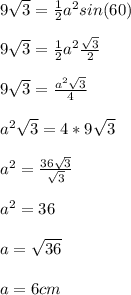
Рассмотрим фигуру BCB'C' - это квадрат образованный гранями a
⇒ диагональ квадрата вычисляется по формуле:
⇒ 
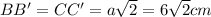
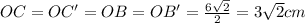
Рассмотрим Δ AOC - это прямоугольный треугольник.
В нем:
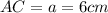- это гипотенуза;
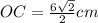- один из катетов.
По Теореме Пифагора:
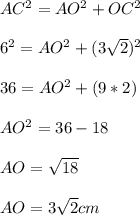
Т.к. наш октаэдр правильный ⇒ AO = OA'
⇒ высота октаэдра:
