ABCD квадрат, следовательно, все его стороны равны между собой, и, в частности, AB=AD.И все углы квадрата по 90 градусов, и, в частности угол DAB = 90 градусов.
Треугольник ADE равносторонний, следовательно все стороны равны между собой, и, в частности, AD=AE. Все углы в равностороннем треугольнике по 60 градусов, следовательно, угол EAD=60 градусам.
Рассмотрим треугольник EAB. Из выше сказанного следует, что AE=AB. Тогда треугольник EAB равнобедренный и углы при основании у него равны: угол BEA=углу ABE. Угол EAB= угол EAD + угол DAB = 60 + 90 = 150 градусов.
Угол BEA = (180 - угол EAB) / 2 =(180 - 150) / 2 = 30 / 2 = 15.
15°, 150° и 15°
Объяснение:
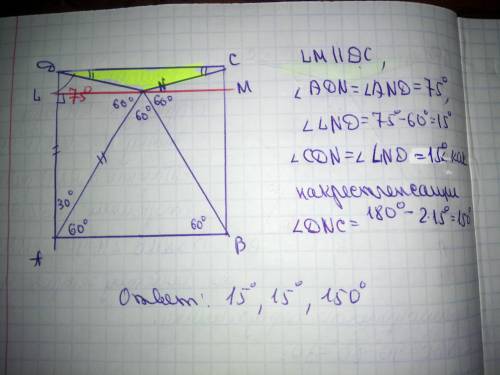
Треугольник ABN - равносторонний, т.е. AB=AN=BN
Но ABCD - квадрат => AB=AN=BN=BC=CD=AD
Рассмотрим треугольник ADN:
<A=90°-<BAN = 90°-60° =30°
AD=AN => треугольник ADN - равносторонний
Значит, <ADN=<AND=(180°-30°)/2 = 75°
Рассмотрим треугольник BCN:
<B=90°-<ABN = 90°-60° =30°
BC=BN => треугольник BCN - равносторонний
Значит, <BNC=<BCN=(180°-30°)/2 = 75°
Рассмотрим треугольник DNC:
<CDN = 90°-<ADN = 90°-75° = 15°
<DCN = 90°-<BCN = 90°-75° = 15°
<DNC = 360° -<AND-<ANB-<BNC = 360°-75°-60°-75° = 150°


пусть ребро куба равно "а" тогда
А₁(0,0,0), А ( 0,0,а), В ( а, 0,а), М ( 0,а, 0,5а) Д₁ (0,а, 0)
1) Найдём координаты векторов
АД₁( 0,а, -а) и ВМ ( -а, а, -0,5а)
2) Найдём их длины
| АД₁|² = 0²+а² +а² = 2а² тогда | АД₁| =а√2
| ВМ|² = а²+а² +0,25а² = 2,25а² тогда | АД₁| =1,5а
3) cosα = ( 0+а² +0,5а² ) / а√2*1,5а = 1/√2
тогда α =45 градусов ( это угол между векторами)