Прямые KC и AD являются скрещивающимися, то есть не лежат в одной плоскости. Но известно, что в качестве угла между скрещивающимися прямыми a и b надо брать меньший из четырех углов пресекающихся прямых a и c, где прямая c параллельна прямой b. В нашем случае в качестве прямой c надо взять прямую BC.
Итак, искомый угол
При этом Угол KCB найдем по свойству внутренних углов треугольника:
Построим сумму векторов а и b и их разность. ↑АС = ↑р = ↑а + ↑b ↑DB = ↑q = ↑a - ↑b Чтобы найти угол между векторами p и q, построим вектор, равный вектору q, с началом в точке А. ∠ЕАС - искомый. Из ΔABD найдем длину вектора q по теореме косинусов: |↑q|² = AB² + AD² - 2·AB·AD·cos60° = 25 + 64 - 2·5·8·1/2 = 89 - 40 = 49 |↑q| = 7 Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°, значит ∠АВС = 120°. Из ΔABС найдем длину вектора р по теореме косинусов: |↑p|² = AB² + BC² - 2·AB·BC·cos120° = 25 + 64 + 2·5·8·1/2 = 89 + 40 = 129 |↑p| = √129
Из ΔЕАС по теореме косинусов: cos α = (AE² + AC² - EC²) / (2 · AE · AC) cos α = (49 + 129 - 256) / (2 · 7 · √129) = - 78 / (14√129) = - 39√129 / 903 cos α = - 13√129/301
Прямые KC и AD являются скрещивающимися, то есть не лежат в одной плоскости. Но известно, что в качестве угла между скрещивающимися прямыми a и b надо брать меньший из четырех углов пресекающихся прямых a и c, где прямая c параллельна прямой b. В нашем случае в качестве прямой c надо взять прямую BC.
Итак, искомый угол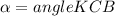
При этом Угол KCB найдем по свойству внутренних углов треугольника:
угол KCB= 180 градусов - (угол KBC + угол BKC)=180 - (100+32)= 48 градусов
Таким образом,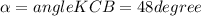
где - угол
- угол  - градус
- градус