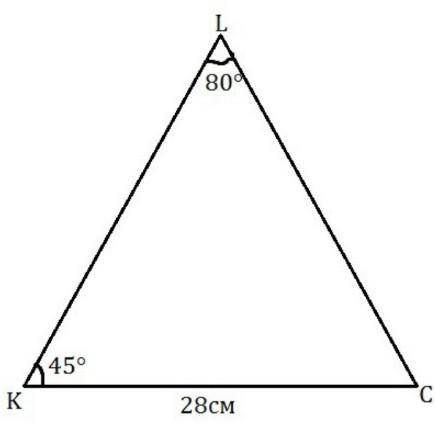
площадь треугольника:
S= \frac{1}{2} *KC*LC*sin(C)S=
2
1
∗KC∗LC∗sin(C)
находим угол C
угол C=180-80-45=55°
найдем сторону LC по теореме синусов:
\begin{lgathered}\frac{sin(45^{\circ})}{LC} = \frac{sin(80^{\circ})}{28} \\LC= \frac{28*sin(45^{\circ})}{sin(80^{\circ})}\end{lgathered}
LC
sin(45
∘
)
=
28
sin(80
∘
)
LC=
sin(80
∘
)
28∗sin(45
∘
)
подставим в формулу площади:
S= \frac{1}{2} *28*\frac{28*sin(45^{\circ})}{sin(80^{\circ})}*sin(55^{\circ})= \frac{14*28*sin(45^{\circ})*sin(55^{\circ})}{sin(80^{\circ})}S=
2
1
∗28∗
sin(80
∘
)
28∗sin(45
∘
)
∗sin(55
∘
)=
sin(80
∘
)
14∗28∗sin(45
∘
)∗sin(55
∘
)
найдем приблизительные значения синуса(например, по таблице Брадиса )
\begin{lgathered}sin(45^{\circ})\approx0,70 \\sin(55^{\circ})\approx 0,82 \\sin(80^{\circ})\approx 0,98\end{lgathered}
sin(45
∘
)≈0,70
sin(55
∘
)≈0,82
sin(80
∘
)≈0,98
подставим эти значения в выражение и найдем площадь:
S= \frac{14*28*0,7*0,82}{0,98} = \frac{14*28*7*82}{98*10} = \frac{7*2*4*7*7*2*41}{7*7*2*10} = \frac{7*4*41*2}{10} =229,6S=
0,98
14∗28∗0,7∗0,82
=
98∗10
14∗28∗7∗82
=
7∗7∗2∗10
7∗2∗4∗7∗7∗2∗41
=
10
7∗4∗41∗2
=229,6
ответ: S=229,6 см
Объяснение:
1. Строим перпендикуляр. Один из углов треугольника- 30 градусов, следовательно противолежащий, нужный нам, катет равен половине гипотенузы или 2 см
2. Строим перпендикуляр. На рисунке изображен треугольник с двумя равными углами, следовательно, он равнобедренный, следовательно высота, которую мы провели, является также медианой. То есть расстояние от середины основания треугольника до точки С- 7см. По сумме острых углов прямоугольного треугольника находим второй острый угол и видим, что он равен первому. То есть треугольник равнобедренный и длина искомого перпендикуляра также равна 7 см.
3. Строим перпендикуляр. Получившийся катет лежит напротив угла в 30 градусов и, следовательно, равен половине гипотенузы или m\2.
4. Большой треугольник равнобедренный, следовательно, его углы при основании равны. То есть угол NKA равен 30 градусов.(180-60=120. 120\2=60. 60\2=30.Опустим перпендикуляр из точки А на прямую а. Получили прямоугольный треугольник с углом в 30 градусов. То есть длина искомого перпендикуляра равна половине длины отрезка КА и равна 3,5 см.