1)Косинус угла между векторами, зная их координаты вычисляется по формуле:
cos α = 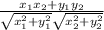
Здесь x1,x2, y1, y2 - координаты двух векторов.
Подставив в эту формулу координаты, получим:
cos α = (0 * 20 + 60) / √16 * √(20² + (-15)²) = 60 / 4 * √625 = 60 / 4 * 25 = 60/100 = 0.6
3)Доказать этот факт несложно. Достаточно соединить эти точки отрезками и доказать, что BA и BC будут перпендикулярными. Тогда мы докажем, что угол между векторами будет равен 90°, то есть они будут перпендикулярными. Теперь найдём каждую из этих сторон.(AB, BC,AC). Это можно сделать, воспользовавшись методом координат, используя извстную формулу, которую я здесь приводить не буду,(вы можете вполне сами найти её в интернете, а сразу проведу вычисления по ней, чтобы не загромождать место.
AB = √((2 - 0)² + (3 - 1)²) = √(4 + 4) = √8
BC = √((-1 - 2)² + (6 - 3)²) = √(9 + 9) = √18
AC = √(-1)² + (6 - 1)² = √(1 + 25) = √26
Теперь заметим, что (√26)² = (√18)² + (√8)², то есть сумма квадрата одной стороны равна сумме квадратов двух других сторон(это обратная теорема Пифагора), значит данный треугольник является прямоугольным, причём по длине сторон можно заключить, что AC - гипотенуза, тогда AB и BC - катеты, которые взаимно перпендикулярны. Итак. мы доказали, что между данными векторами прямой угол, значит они перпендикулярны между собой, что и требовалось доказать.
Проанализируем каждое утверждение :
1) Ромб - частный случай параллелограмма. Площадь параллелограмма равна произведению смежных сторон на синус угла между ними. Точно также можно сказать и про ромб.
ответ: утверждение 1 верно.
2) В равнобедренном треугольнике биссектриса, проведённая к основанию - медиана и высота. Биссектриса, проведённая к боковой стороне не всегда является также медианой (только в равностороннем треугольнике, но ведь равнобедренный треугольник не всегда является равносторонним).
ответ: утверждение 2 неверно.
3) Сумма углов треугольника равна 180°. Сумма ВНЕШНИХ углов треугольника равна 360°.
ответ: утверждение 3 неверно.
ответ: 1).
Н - высота пирамиды
h - высота основания пирамиды
r -радиус окружности, вписанной в основание
а - сторона основания
Решение
а) высота пирамиды Н = L· sinβ
б) проекция апофемы на плоскость основания -это радиус вписанной окружности r = L · cosβ.
в) сторона основания пирамиды а = 2r/tg 30° = 2L· cosβ/(1/√3) =
= 2√3 · L·cosβ
г) площадь основания пирамиды Sосн = 0.5h·a, где h = a·cos30°.
Тогда Sосн = 0.25a²·√3 = 0.25 · √3 · (2√3 · L·cosβ)² = 3√3L² · cos²β
д) Площадь боковой поверхности пирамиды
Sбок = 3 · 0,5 · L · a = 1.5L · 2√3 · L·cosβ = 3√3 · L² · cosβ
e) площадь полной поверхности пирамиды:
Sполн = Sосн + Sбок = 3√3 · L² · cos²β + 3√3 · L² · cosβ =
= 3√3 · L² · cosβ · (cosβ + 1)