Боковое ребро наклонной призмы равно 14 см и составляет с плоскостью основания угол 30º. Нужно найти высоту призмы.
-------------
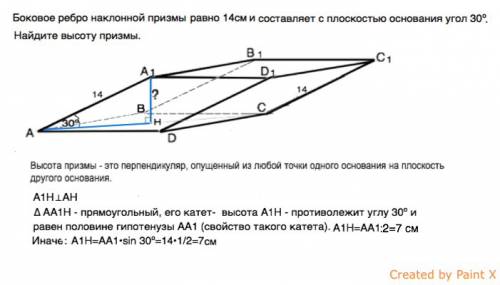
Высота призмы - это перпендикуляр, опущенный из любой точки одного основания на плоскость другого основания.
Т.к. основания лежат в параллельных плоскостях, высота призмы равна расстоянию между плоскостями, содержащими её основания.
Обозначим вершины призмы ABCDA1B1C1D1 (см.рисунок в приложении)
Опустим из вершины А1 перпендикуляр А1Н на плоскость основания.
А1Н ⊥АН
∆ АА1Н - прямоугольный, его катет- высота призмы А1Н - противолежит углу 30º и равен половине гипотенузы АА1.
А1Н=14:2=7 см
Иначе: А1Н=АА1•sin 30º=14•1/2=7см
–––––––––
Примечание:
Высота призмы не обязательно совпадает с высотой боковой грани. Она совпадает с ней, только если призма прямая. В данном случае призма - наклонная.
cos∠B = (BA² + BC² - AC²) / (2·BA·BC)
cos∠B = (64 + 81 - 100) / (2·8·9) = 45/ (2·8·9) = 5/16 = 0,3125
∠B ≈ 71,5°
cos∠A = (AB² + AC² - BC²) / (2·AB·AC)
cos∠A = (64 + 100 - 81) / (2·8·10) = 83 / 160 ≈ 0,5188
∠A ≈ 59°
∠C = 180° - (∠A + ∠B)
∠C ≈ 180° - (59° + 71,5°) ≈ 180° - 130,5° ≈ 49,5°