Вариант ответа 5
Объяснение:
Это больше теоретический вопрос.
Координаты середины отрезка есть среднее арифметическое между соответствующими координатами концов отрезка. Обозначим О1(х1;у1), О2(х2;у2), О3(х3;у3), где О2-середина отрезка О1О3. Составим уравнения для нахождения координат середины отрезка: х2=(х1+х3)/2, у2=(у1+у3)/2. В данных уравнениях известны х2 и х3, у2 и у3. Нужно найти х1 и у1.
х2=(х1+х3)/2, 2х2=х1+х3, х1=2х2-х3 подставим значения: х1=2×7-13=1.
у2=(у1+у3)/2, 2у2=у1+у3, у1=2у2-у3 подставим значения: у1=2×(-2)-4=-8
О(1;-8)- искомая.
ответ:Для начала необходимо вспомнить, что нам известно о тангенсе угла и как его можно вычислить.
Первое, что приходит в голову, – это, конечно же, вычисление значения тангенса с сторон прямоугольного треугольника. В прямоугольном треугольнике тангенс острого угла находится как деление катета, который расположен напротив этого угла, на катет, который прилегает к рассматриваемому углу.
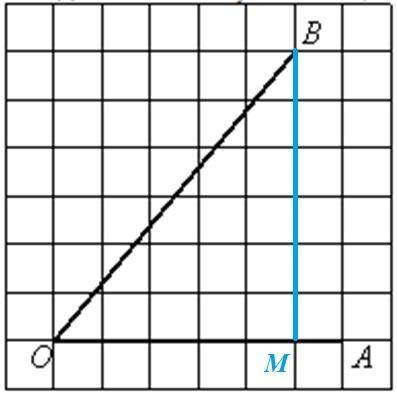
Посмотрим на рисунок.
Нужно найти тангенс острого угла АОВ. Длину стороны ОА найти можно по клеточкам. Чтобы получить второй катет, нужно опустить из точки В на сторону ОА перпендикулярную прямую, которая пересечет сторону ОА в точке. Назовем эту точку буквой М.
Из полученного прямоугольного треугольника ВОМ по клеточкам возможно узнать длину обоих катетов (посчитать количество клеточек).
Итак, длина прилегающего к углу АОВ катета ОМ равна 5 клеточкам (назовем их условн. единицами), а длина противолежащего катета ВМ равна 6 условных единиц.
Найдем тангенс острого угла АОВ:
tg AOB = BM / OM = 6 / 5 = 1,2
ответ. 1,2.
Объяснение: