при ВС ∥АД и секущей СО
Но угол ВСО=углу ОСД по условию.
Значит, в треугольнике СОД угол СОД=углу ОСД и треугольник ОСД - равнобедренный
ОД=СД=17
2 Угол ВОА=углу ОВС как накрест лежащие при ВС ∥АД и секущей ВО
Но угол ОВС = углу АВО по условию
Значит, в треугольнике АВО углы при основании равны и он - равнобедренный.
АВ=АО=10
3. АД= АО+ОД=10+17=27
4. В прямоугольном треугольнике АВК найдем АК по теореме Пифагора.
АК =корень из ( 10^2-8^2)=6
5. В прямоуг. треугольнике МСД найдем МД по теореме Пифагора
МД = корень из ( 17^2-8^2)=15
6.ВС= АД-АК-МД=27-6-15=6
7.Ищем площадь классически - полусумма оснований на высоту. S авсд= (6+27 *8)/2=132
234
Объяснение:
Допустим дана трапеция ABCD, угол ВАС - прямой, биссектриса проведена из угла CDA, АВ=12см, CD=15см. Т.к. биссектриса делит угол пополам, то угол СDB равен углу BDA.
Угол BDA равен углу DBC как накрестлежащий. Следовательно CDB=BDA=DBC. Значит треугольник DBC - равнобедренный и сторона CD равна стороне BC, значит BC=15 см.
Проведем высоту СН к основанию AD. Т.к. трапеция прямоугольная CH=AD=12см. У нас получился прямоугольный треугольник CHD, в котором известно CH=12см, CD=15см.
Нужно найти катет HD.
Используем формулу для нахождения гипотенузы в прямоугольном треугольнике 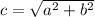
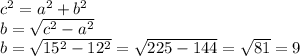
Т.к. ABCH - прямоугольник, то ВС=АH=15см. Из этого следует, что AD=15+9=24. Т.к. трапеция прямоугольная, то сторона AB - высота.
Найдем площадь трапеции по формуле 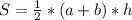
S=1/2*(15+24)*12=6*39=234
13,5=под корнем 4х в квадрате + 2,25х в квадрате
13,5=2,5х
х=5,4
тогда 1 диагональ = 16,2 см
2 диагональ = 21,6 см