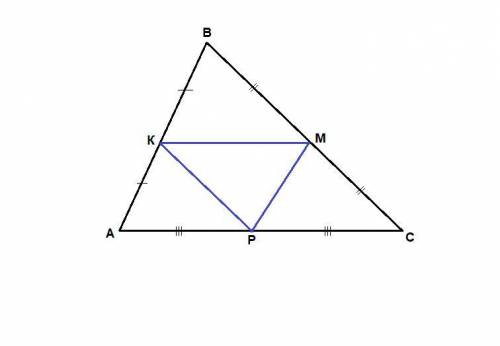
Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине.
МР = АВ/2, ⇒
МР = АК = КВ
КР = ВС/2, ⇒
КР = ВМ = МС
КМ = АС/2, ⇒
КМ = АР = РС.
Таким образом ΔАКР = ΔКВМ = ΔРМС = ΔМРК по трем сторонам.
Для ΔАКР и ΔАВС:
∠А - общий,
∠АКР = ∠АВС как соответственные при пересечении параллельных прямых КР и ВС секущей АВ, значит
ΔАКР подобен ΔАВС по двум углам.
Значит треугольнику АВС будут подобны и все остальные треугольники, равные треугольнику АКР:
ΔКВМ подобен ΔАВС
ΔРМС подобен ΔАВС
ΔМРК подобен ΔАВС
1. Угол между наклонной к плоскости и плоскостью - это угол между наклонной и ее проекцией на плоскость. Искомый угол - угол МАО. Высота правильного треугольника равна h=(√3/2)*a = (√3/2)*2√3=3. АО=(1/3)*h = 1 (свойство медианы). Tg(<MAO) = MO/AO = √3.
ответ: α = arctg√3 = 60°
2. Искомый угол - угол между наклонной и ее проекцией, то есть угол АВК. Sin(<ABK) = KA/KB = AC*tg60/5 = 5√3/11. <ABK = arcsin(0,787) ≈ 51,9°.
3. Опустим перпендикуляры SP и SH из точки S к сторонам АВ и АD соответственно. Прямоугольные треугольники APS и AHS равны по гипотенузе и острому углу. Значит АР=АН и АРОН - квадрат. тогда АО = АН*√2 (диагональ квадрата), АS = 2*АН (в треугольнике ASH катет АН лежит против угла 30°, а AS - гипотенуза). Косинус искомого угла (между наклонной AS и плоскостью АВСD, равного отношению проекции наклонной к наклонной) = АО/AS = АН√2/(2*АН) = √2/2.
ответ: искомый угол равен 45°.

По свойству параллелограмма - его противолежащие стороны равны:
АВ=СD = х см
ВС=AD = (х+4) см
Периметр параллелограмма:
2 * (х + х+4) = 64
2х + 4 = 64 : 2
2х + 4 = 32
2х = 32 - 4
2х = 28
х = 28:2
х = 14 (см) ⇒ АВ=СD = 14 см
ВС=AD = 14 + 4 = 18 (см)
ответ: АВ=СD=14 см , ВС=AD= 18 см.