Один угол параллелограмма больше другого на 78 градусов. Найдите больший угол ответ дайте в градусах.
По признаку параллелограмма - противоположные углы параллелограмма одинаковые. Значит:
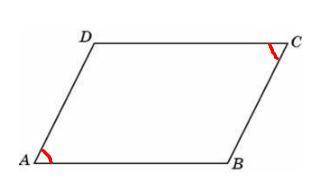
∠DAB = ∠DCB и ∠ADC = ∠CDA.
Пользуясь еще одним важным свойством параллелограмма - сумма углов параллелограмма прилегающих к любой стороне равна 180° - составим уравнение.
Пусть меньший угол параллелограмма - x градусов. Тогда больший - (x+78) градусов. Так как их сумма 180° имеем:
x + x + 78 = 180
2x = 180 - 78
2x = 102
x = 102 : 2
x = 51
Таким образом меньший угол фигуры равен 51°.
Тогда больший: 51 + 78 = 129°
ответ: 129°
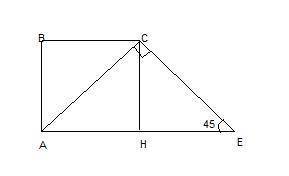
В прямоугольных ΔABH и ΔCDK ∠ABH=∠DCK=90°-60°=30°
По свойству угла в 30° в прямоугольном треугольнике, AH=KD=22/2=11
тогда
AD+BC=BC+BC+AH+KD=2BC+2AH
2BC+2AH=86
BC+11=43
BC=32
и
AD=BC+2AH=32+2·11=54
ответ: 32см и 54см