
Даны координаты A(7,7,3), В(6,5,8), С(3,5,8) и D(8,4,1).
Находим векторы:
x y z Квадрат Длина ребра
Вектор АВ={xB-xA, yB-yA, zB-zA} -1 -2 5 30 5,4772
Вектор АC={xC-xA, yC-yA, zC-zA} -4 -2 5 45 6,7082.
Их векторное произведение равно: АВ х АС =
= i j k | i j
-1 -2 5 | -1 -2
-4 -2 5 | -4 -2 = -10i - 20j + 2k + 5j + 10i - 8k =
= 0i - 15j - 6k = (0; -15; -6).
Площадь основания (АВС) равна половине модуля:
S(ABC) = (1/2)*√(0 + 225 + 36) = (1/2)*√261 = (3/2)√29 ≈ 8,0778.
Находим вектор AD:
Вектор АD={xD-xA, yD-yA, zD-zA (1 -3 -2) = √ 14 ≈ 3,742.
Находим смешанное произведение:
АВ х АС = (0; -15; -6).
АD = (1; -3; -2).
(АВ х АС) * АD = 0 + 45 + 12 = 57.
Объём пирамиды равен (1/6) смешанного произведения:
V = (1/6)*57 = 57/6 = 19/2 = 9,5 куб.ед.
Теперь определяем искомую высоту из вершины D на АВС.
Н = 3V/S(ABC) = 3*(19/2)/((3/2)√29) = 19√29/29 ≈ 3,528.
Ответ: 6 см
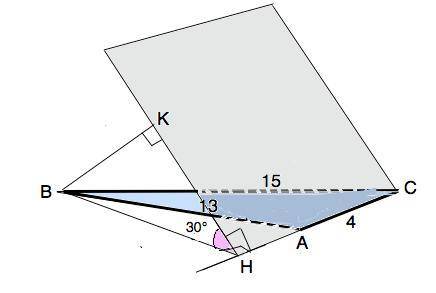
Объяснение: Угол между плоскостями — это угол между перпендикулярами, проведенными в этих плоскостях к одной точке на линии их пересечения.
Линия пересечения - прямая СА, перпендикуляры к ней НВ и НК. Угол ВНК=30°(дано)
ВН - высота ∆ АВС к стороне АС. Площадь ∆ АВС по формуле Герона равна 24 см².
Из формулы площади треугольника высота ВН=2Ѕ:АС=48:4=12 (см).
Расстояние от точки до плоскости измеряется длиной перпендикуляра, опущенного из той точки на плоскость.
Из прямоугольного ∆ ВКН искомое расстояние ВК=ВН•sin30°=12•1/2=6 см
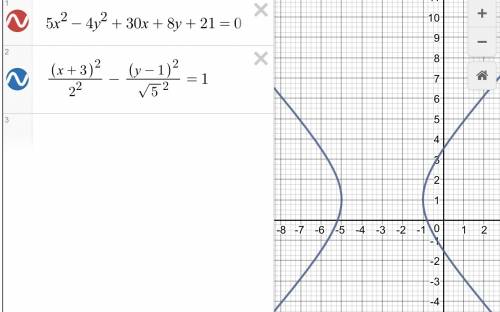
5x² - 4y² + 30x + 8y + 21 = 0.
Выделяем полные квадраты:
5(х + 3)² - 4(у² - 1)² = 20.
Делим обе части уравнения на 20 и получаем каноническое уравнение гиперболы:
((х + 3)²/(2²)) - ((у² - 1)²/(√5)²) = 1.
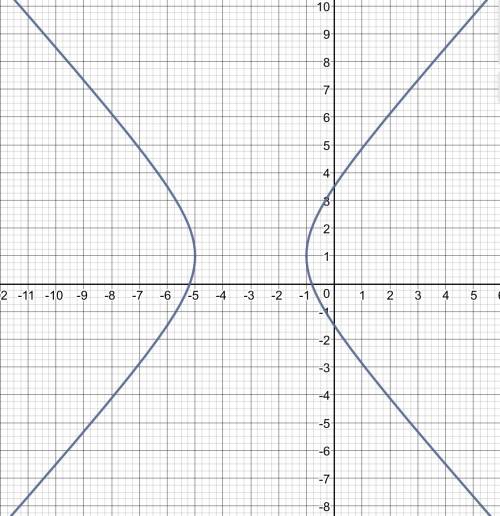
Данное уравнение определяет гиперболу с центром в точке:
C(-3; 1) и полуосями: а = 2 и b = √5.
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
Определим параметр c: c² = a² + b² = 4 + 5 = 9.
c = 3.
Тогда эксцентриситет будет равен: ε = с/а = 3/2.
Асимптотами гиперболы будут прямые:
у - 1 = (√5/2)(х + 3) и у - 1 = -(√5/2)(х + 3).
Директрисами гиперболы будут прямые:
х + 3 = а/ε ,
х + 3 = +-(2/(3/2)).
х + 3 = +-(4/3).
График и таблица координат точек для его построения приведены в приложении.