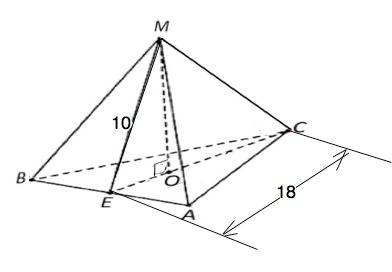
В правильной пирамиде все грани – равнобедренные треугольники и равны, а высота проецируется в центр основания - точку пересечения высот(медиан). По свойству медианы эта точка делит их в отношении 2:1, считая от вершины. Обозначим данную пирамиду МАВС. Высота МО, апофема МЕ=10, высота основания СЕ=18..
Высота основания СЕ делится на отрезки СО=18•2/3=12, ОЕ=18:3=6
Треугольник МОЕ прямоугольный и по отношению катета ОЕ и гипотенузы МЕ - египетский.
Поэтому высота пирамиды МО=8 ( можно найти по т.Пифагора).
Пусть AE высота треугольника ACD. Заметим, что в прямоугольных треугольниках OHA и EHD острые углы OHA и EHD равны как вертикальные. А значит, равны и вторые острые углы этих треугольников:
EDH=ОAH. Из этого равенства и равенства углов CAB=CDB получаем, что BAO=HAO. А значит, AO – биссектриса треугольника ABH, но она же и высота этого треугольника (диагонали перпендикулярны). И поэтому треугольник ABH равнобедренный. AO - его медиана. BO=OH, ВO=HD (по условию) и значит OH=HD и H – середина отрезка DO.

Былины рассказывают нам о подвигах и приключениях богатырей и героическом русской истории. Они были созданы много веков назад. Многие из них навсегда затерялись во времени.
Мне нравятся былины, которые рассказывают о подвигах русских богатырей. Мой любимый былинный герой – Илья Муромец. Как гласит былинная история, до 33 лет Илья был болен и не мог ходить. Но потом он чудесным образом обрёл здоровье и богатырскую силу.
Илья Муромец - настоящий защитник родной земли. Он бережет Родину от врагов и захватчиков. Он смелый, отважный и необычайно сильный. Илья Муромец всегда приходит на слабым и бес Он честный и справедливый, всегда говорит правду и отстаивает её даже перед князем и боярами.
Об Илье Муромце сложено множество былин. Это говорит об огромной народной любви к этому персонажу. Илья Муромец – настоящий герой, воплотивший в себе все лучшие качества, совершивший необычайные подвиги и бескорыстно служивший на благо родной земли.