Угол α между вектором a и b (формула):
cosα=(Xa*Xb+Ya*Yb+Za*Zb)/[√(Xa²+Ya²+Xa²)*√(Xb²+Yb²+Zb²)].
Следовательно, надо найти координаты векторов СА и СВ и по приведенной выше формуле вычислить косинус угла между этими векторами.
Координаты вектора равны разности соответствующих координат точек его конца и начала ab{х2-х1;y2-y1;z2-z1}.
Вектор СА{6-1;2-(-5);4-8} ={5;7;-4},
Bектор СВ{-3-1;5-(-5);-7-8} = {-4;10;-15}. Тогда
cos(CA^CB) = (5*(-4)+7*10+(-4)*(-15))/[√(25+49+16)*√(16+100+225)] = 0,6279.
<ACB = arccos(0,6279) ≈ 51,1°. Это ответ.
Или по теореме косинусов:
Найдем длины сторон треугольника АВС (модули векторов) АВ, СA и СB, зная их координаты.
Вектор АВ{-9;3;-11}, вектор СА{5;7;-4}, вектор СВ{-4;10;-15}.
|AB|=√(81+9+121) = √211
|CA|=√(25+49+16) = √90
|CB|=√(16+100+225)=√341.
Тогда по теореме косинусов:
Cos(CA^CB)=(90+341-211)/(2*√90*√341) = 220/350,4 ≈ 0,6279.
ответ тот же, что и в первом случае.
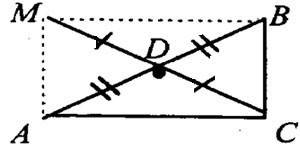
А прямая будет параллельна основанию потому, что отсекаются половины сторон. То есть отрезанный треугольник будет в два раза меньше, чем был первый.