Изи
Объяснение:
Задача1:
1)угол MOK(центральный)=дуге MK=78°
2)угол ONK(вписаный)= половине дуги MK=78°:2=39°
3)угол NOK( | радиусу):(по теореме о касательных)
=>(следовательно)=90°
угол x: угол ONK+угол NOK+угол x=180°
( переделаем под угол формулу):
Угол х=180°-(39°+90°)=180°-129°=51°
Задача2:
НЕ ЗНАЮ(((
ПОЯСНЕНИЕ ОБЯЗАТЕЛЬНО ПРОЧИТАЙ,ЧТОБЫ В ДАЛЬНЕЙШЕМ ПОНИМАТЬ,ЧТО Я ПИШУ,ТАК КАК ВРЕМЯ ДЕНЬГИ, ТО:
ВПИСАННЫЙ УГОЛ-В
ЦЕНТРАЛЬНЫЙ УГОЛ0-Ц
РАДИУС-Р
Диаметр-Д
Дуга-д
Угол-У
Половина- п
Известны дуги сумма дуг =360°
=> д KM+д ML+д KL=360°
=> д KL=360°-(д KM+д ML)=360°-(77°+143°)=360°-220°=140°
У M(ВУ:=П д)=140°÷2=70°
Задача10:
Не знаю чего-то не могу увидеть вижу только:
MN-Д
У MKN=90 опирается на Д и по теореме касательных тоже
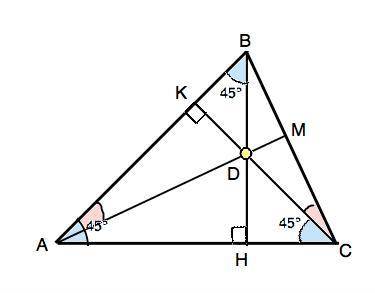
Внутри треугольника АВС взята точка D такая, что угол ABD = угол ACD = 45°. Докажите, что отрезки AD и BC перпендикулярны и равны, если угол ВАС равен 45°
* * *
Продлим ВD до пересечения с АС в т.Н, а отрезок СD - до пересечения с АВ в т.К и проведем АМ через т.D.
∠АСD=45° по условию, Если ∠ВАС=45°, то ∠АКС=90° и ∆ АСК – равнобедренный прямоугольный. АК=СК.
В ∆ АВН два угла при АВ равны 45°⇒∠ВНА=90° и ∆ АВН - равнобедренный прямоугольный, Тогда точка D - пересечение высот СК и ВН треугольника АВС. Отрезок АМ, содержащий АD, проходит через точку пересечения высот, следовательно, является высотой и перпендикулярен ВС. Отсюда АD⊥ВС. Доказано.
Прямоугольные ⊿ АКD и ⊿ CMD подобны по равному углу при вершине D ( вертикальные) ⇒ ∠КАD=∠MCD.
Рассмотрим ⊿ АКD и ⊿ ВКС. Из ⊿ АКС их катеты АК=СК. Острые ∠КАD и ∠КСВ равны (из доказанного выше). Следовательно, ⊿ АКD=⊿ ВКС по катету и острому углу. Отсюда следует равенство гипотенуз этих треугольников. АD=ВС, ч.т.д.