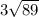
Объяснение:
Объём пирамиды:
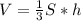, где S - площадь основания, h - высота пирамиды.
Значит 
У правильной четырёхугольной пирамиды основанием выступает квадрат. Если сторону квадрата обозначить как а, то S=a² ⇒ а=√S.
Боковое ребро пирамиды l, её высота h и полудиагональ основания образуют прямоугольный треугольник, в котором искомое ребро - гипотенуза, а высота и полудиагональ - катеты.
Диагональ квадрата равна √(2а²)=а*√2,
тогда половина диагонали равна а/√2, а так как а=√S,
то половина диагонали равна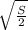 
Тогда, по теореме Пифагора:
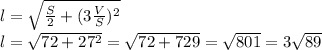
площадь квадрата = R2*1/2, где R - радиус описанной окружности.
Вычислим площадь квадрата через площади трёх треугольников образованные центром окружности и вершинами треугольника.
Угол с вершиной в центре окружности в каждом треугольнике 120,
тогда площадь искомого треугольника равна.
S = 3 * 1/2 * R*R*sin120C = 3/2 * 2Q *\
/2 = 3*\
*Q/2