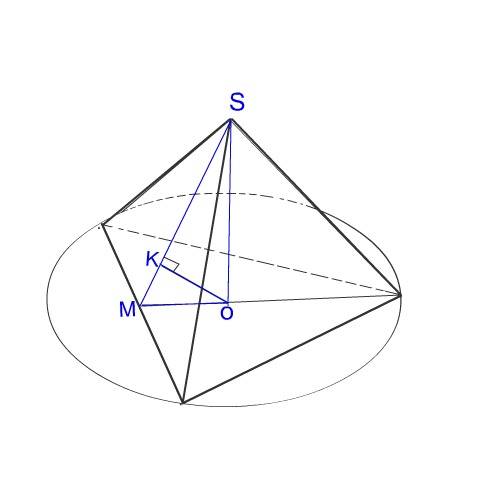
Расстояние от центра описанной около основания этого тетраэдра окружности до грани - перпендикуляр к этой грани.
На рисунке - это отрезок ОК.
Центр описанной около правильного треугольника окружности ( а грани правильного тетраэдра - правильные треугольники) лежит на пересечении высот треугольника на расстоянии одной трети высоты от стороны.
Найдем высоту треугольника по формуле
h=a√3):2, а так как а=1,то
h= √3):2
ОМ=√3):2):3=√3):6
Так как все грани правильного тетраэдра равны,
SM равна h=√3):2
Расстояние КО будем находить из прямоугольного треугольника SОМ
Применим теорему:
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.
Здесь этот катет - ОМ
ОМ²=МК·SM
(√3):6)²=МК·(√3):2)
МК=3/36:(√3):2)=6/36):√3=1/6√3
ОК²=МО²-КМ²
ОК²=3/36 -1/108=9/108-1/108=8/108=2/27=6/81
ОК =√(6/81)=√6):9
Если боковые грани наклонены под углом 45 градусов, значит боковой треугольник- прямоугольный, и катеты его будут равные. По теореме Пифагора найдём катеты. обозначу один катет-А, другой-В, гипотинуза-С. Получим А^2 + B^2=C^2. Так как А=В запишем 2А^2=100; А^2=50; A=корень из 50.
Итак боковая грань = корень из 50. проведём высоту и соединим с боковой гранью. Получим прямоугольный треугольник, где боковая грань является гипотинузой, а высота катетом. У этого треугольника катеты так же будут равны, поэтому по предыдущей формуле найдём: 2А^2=50; А^2=25; А=5.
ответ: высота =5.
АВ=ВС
ПРОВЕДЕМ ВЫСОТУ ВН-ОНА ЯВЛЯЕТСЯ И БИССЕКТРИСОЙ,ЗНАЧИТ АН=СН
АН=30
РАССМОТРИМ ТРЕУГОЛЬНИК АВН-ОН ПРЯМОУГОЛЬНЫЙ,ЗНАЧИТ
с^2=а^2+b^2(теорема Пифагора)
50^2=30^2+b^2
b^2=2500 - 900=1600
b=40
BH=40
S=1/2ВН×AC
40×60:2=1200