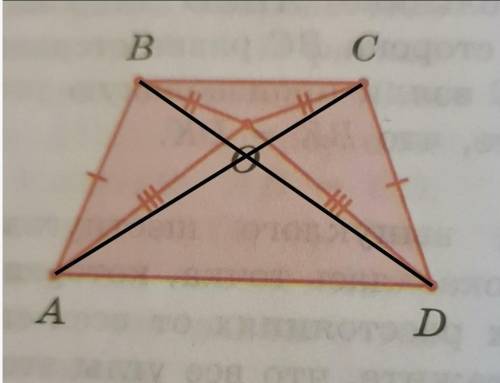
Рассмотрим ∆BOA и ∆COD.
BO=CO по условию;
AB=CD по условию;
АО=DO по условию;
Следовательно ∆ВОА=∆COD по трём сторонам.
Исходя из равенства: угол АВО=угол DCO как соответственные углы равных треугольников. Пусть каждый из этих углов равен х.
Так как ВО=СO, то ∆ВОС – равнобедренный с основанием ВС.
Углы при основании равнобедренного треугольника равны, то есть угол СВО=угол ВСО.
Пусть каждый из них равен z.
Угол АВС=угол АВО+угол СВО=х+z;
Угол DCB=угол DCO+угол ВСО=х+z;
Получим что угол АВС=угол DCB.
Рассмотрим ∆АВС и ∆DCB.
ВС – общая сторона;
Угол АВС=угол DCB (доказано ранее)
АВ=CD по условию;
Следовательно ∆АВС=∆DCB по двум сторонам и углу между ними.
Значит АС=BD как соответственные стороны равных треугольников.
Доказано.
. ∠ALB и ∠ALC — смежные, тогда:
∠ALB + ∠ALC = 180°.
Таким образом:
∠ALB + 121° = 180°;
∠ALB = 180° - 121°;
∠ALB = 59°.
2. Рассмотрим △ABL:
∠LAB + ∠ABL (он же ∠ABC) + ∠ALB = 180° (по теореме о сумме улов треугольника).
Таким образом:
∠LAB + 101° + 59° = 180°;
∠LAB = 180° - 160°;
∠LAB = 20°.
3. Так как AL — биссектриса, то:
∠LAB = ∠LAC.
Таким образом:
∠LAC = 20°.
4. Рассмотрим △ALC:
∠LAC + ∠ALC + ∠ACL = 180° (по теореме о сумме улов треугольника)/
Таким образом:
20° + 121° + ∠ACL = 180°;
∠ACL = 180° - 141°;
∠ACL = 39°.
∠ACL = ∠ACB = 39°.
ответ: ∠ACB = 39°.