Спо стереометрии. основания призмы abca1b1c1— равносторонние треуголь-ники. точки m и m1— центры оснований abc и a1b1c1соответ-ственно.а) докажите, что угол между прямыми bm и c1m1равен 60◦.б) найдите угол между прямыми bm1и c1m, если призма прямаяи ab : aa1=3: 2. p.s. оба пункта сделать , особенно в б не понимаю где угол между скрещивающимися прямыми окажется.

👇

Ответ:

gjkbyf6789

30.06.2022

А) С1М1 || СМ угол между СМ и ВМ в правильном треугольнике 60°

б) Пусть АВ =3 ВВ1=2
Пусть В - начало координат
Ось Х - ВС
Ось У - перпендикулярно Х в сторону А
Ось Z - ВВ1

Координаты точек
В(0;0;0)
С1(3;0;2)
М(1.5;√3/2;0)
М1(1.5;√3/2;2)

Вектора
ВМ1(1.5;√3/2;2) длина √(9/4+3/4+16/4)=√7
С1М(-1.5;√3/2;-2) длина тоже √7
косинус искомого угла
| ВМ1*С1М | / | ВМ1 | / | С1М | = | -9/4+3/4-16/4 | / 7 = 22/28= 11/14
угол arccos(11/14)

4,4(13 оценок)

Открыть все ответы

Ответ:

ViktoriyaFomina1

30.06.2022

Объяснение:

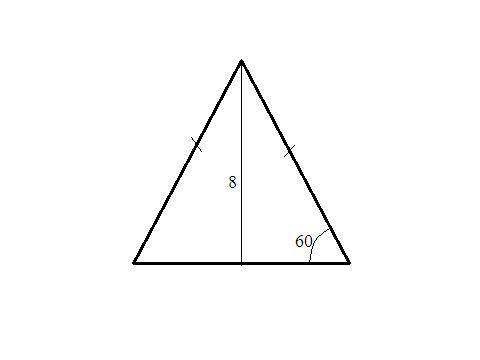
Осевое сечение конуса - равнобедренный треугольник с боковыми сторонами (образующие конуса), основание - диаметр основания.

Треугольник, образованный высотой, образующей и половиной диаметра - прямоугольный. Угол при вершине (90-60)=30° ⇒ половина диаметра (катет против угла 30°) равен половине образующей (гипотенуза). По т. Пифагора -

(2х)²=8²+х²

х²=8²/3

х=8/√3;

Площадь - S=a*h/2, где а=2х=16/√3, h=8;

S=16*8/(2√3)=64/√3=64√3/3.

Можно проще.

Угол при основании 60° ⇒ треугольник равносторонний.

S=h²/√3=8²/√3=64/√3=64√3/3.

решить задачу по геометрии Найти площадь осевого сечения конуса, высота которого 8 см, а образующая

4,8(63 оценок)

Ответ:

kolodenkoa444

30.06.2022

На чертеже точки касания N и N1 изображены совпадающими, но это еще надо доказать. Поэтому СНАЧАЛА я не считаю их совпадающими. То есть окружность O1 касается AC в точке N, а окружность O2 - в точке N1 (слова "с центром" дальше буду опускать, если и так ясно).
Для треугольника ABC точки касания с O1 делят стороны на три отрезка AN, CN и еще один (точнее, два равных) из вершины B. Я обозначу его например буквой x.
Тогда очевидно
AN + CN = AC;
AN + x = AB;
CN + x = BC;
Если вычесть из второго третье, получится AN - CN = AB - BC; если теперь сложить это с первым, то
AN = (AC + AB - BC)/2;
Точно так же для треугольника ACD получается
AN1 = (AC + AD - CD)/2; и нигде не предполагается, что AN = AN1; это надо доказать.
Весь четырехугольник ABCD является ОПИСАННЫМ, то есть AD + BC = AB + CD;
или AD - CD = AB - BC; или AC + AD - CD = AC + AB - BC; то есть AN = AN1, и точки N и N1 совпадают, это просто одна точка N.
Последствия этого очень велики. :) Окружности O1 и O2 касаются, AC является общей касательной, проведенной в точке касания N окружностей O1 и O2, и линия центров O1O2 перпендикулярна AC.
Важно! - пока нигде не использовано, что ABCD - трапеция! Этот результат справедлив для любого выпуклого описанного четырехугольника.
Поэтому (см. чертеж) ∠KO1O2 = ∠CAD (стороны углов перпендикулярны), и треугольники KO1O2 и ACP подобны. CP - высота трапеции. Она равна
CP = 2R = 40;
сумма радиусов окружностей равна O1O2 = 25; отсюда легко найти KO1 = 40 - 25 = 15; получился "египетский" треугольник :) то есть KO2 = 20;
Ну, и из подобия KO1O2 и ACP AC = 50 (поскольку СP = 2*KO2 :) )
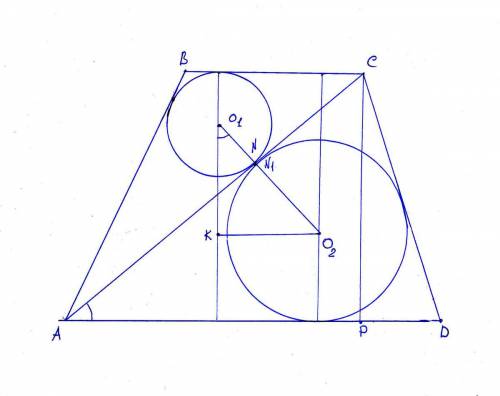
Решить.трапеция abcd описана окло окружности радиуса 20. найти длину диагонали ac трапеции, если рас