Какова градусная мера 1/15 дуги центрального угла равного 90 градусов

👇

Ответ:

Vasianeumaha

29.04.2023

Величина центрального угла равна дуге, на которую он опирается, Следовательно, раз центральный угол 90°, то и градусная мера соответствующей дуги тоже 90°.
Требуется найти 1/15 часть дуги.
90° · 1/15 = 6°
ответ: 6°

4,4(69 оценок)

Открыть все ответы

Ответ:

nikitakomer

29.04.2023

$S_{GHK}= \dfrac{3}{7}$

Объяснение:

Прямоугольник АВСD

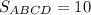
$S_{ABCD} = 10$

BE = EF = FC

AG = GD

-------------------------

$S_{GHK}- ?$

-------------------------

Пусть длинные стороны прямоугольника равны а, а короткие - b.

ВС = AD = a

FD = СВ = b

Тогда площадь прямоугольника

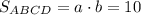
$S_{ABCD} = a\cdot b = 10$

ΔBEH ~ ΔDGH по двум углам (∠BEH = ∠DHG - вертикальные углы; ∠HBE = ∠HDG -внутренние накрест лежащие углы при ВС║AD и секущей BD)

Из подобия этих треугольников следует пропорциональность сторон BE = a/3 и DG = a/2, откуда , что коэффициент подобия

k = a/3 : a/2 = 2/3

Высоты этих треугольников также относятся как 2:3, и высота ΔDGH равна 3b/5. Площадь ΔDGH равна

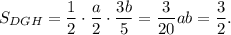
$S_{DGH} = \dfrac{1}{2} \cdot \dfrac{a}{2}\cdot \dfrac{3b}{5} = \dfrac{3}{20}ab = \dfrac{3}{2} .$

ΔBFK ~ ΔDGK по двум углам (∠BKFH = ∠DKG - вертикальные углы; ∠KBF = ∠KDG -внутренние накрест лежащие углы при ВС║AD и секущей BD) .

Из подобия этих треугольников следует пропорциональность сторон BF = 2a/3 и DG = a/2, откуда коэффициент подобия

k = 2/3 : a/2 = 4/3

Высоты этих треугольников также относятся как 4:3, и высота ΔDGK равна 3b/7. Площадь ΔDGK равна

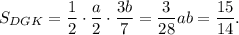
$S_{DGK} = \dfrac{1}{2} \cdot \dfrac{a}{2}\cdot \dfrac{3b}{7} = \dfrac{3}{28}ab = \dfrac{15}{14} .$

Площадь ΔGHK

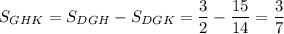
$S_{GHK}= S_{DGH}-S_{DGK}= \dfrac{3}{2} -\dfrac{15}{14} = \dfrac{3}{7}$

4,4(37 оценок)

Ответ:

ankaschamina20

29.04.2023

AM ⊥BM ( AB диаметр большой окружности )
OC ⊥ BM ( OC ⊥ BC ,где O центр малой окружности , BC касательная) ⇒ AM | | OC . MC/CB= AO/OB (обобщенная теорема Фалеса) .
2,4 /4 =r/(2R -r) ⇔   r=3R/4 (1) .
Из ΔBCO по теореме Пифагора :
OB² - OC² =BC² ;
(2R -r)² - r² = 4² ⇔ 4R(R-r) =16 ⇔ R(R-r) =4   (2).
R(R -3R/4) =4 ⇒ R =4. ⇒  r=3R/4 = 3.

AD =AC+CD.
AM =√(AB² -BM²) =√((2R)² -(MC+CB)² ) =√(8² -6,4²) =√(8 -6,4)(8 +6,4) =4,8.
AM можно вычислить по другому: AM/OC =MB/CB ⇔ AM/3 =6,4/4⇒
AM =4,8.
---
AC =√(BC² +AM²) =√(2,4² +4,8²) =√(2,4² +(2*2,4)²) = 2,4√5.
AC*CD = MC*BC ⇔ 2,4√5 *CD =2,4*4⇒ CD =4/√5 =4√5 / 5 =0,8√5.
AD =AC+CD= 2,4√5 + 0,8√5  =3,2√5 .

4,4(39 оценок)

Это интересно:

Кулинария-и-гостеприимство

27.12.2020

Секреты замаринованной бамии: как сделать ее вкусной и полезной...

Компьютеры-и-электроника

28.05.2020

Как играть в PSP игры на Android с помощью приложения PPSSPP...

Без категории

01.10.2021

Как выпустить микстейп: от выбора темы до промоушена...

Хобби-и-рукоделие