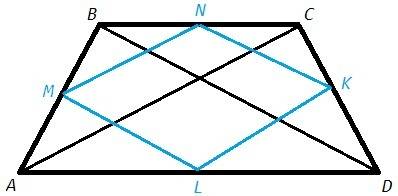
Середины сторон четырехугольника являются вершинами параллелограмма (теорема Вариньона). Стороны параллелограмма Вариньона параллельны диагоналям четырехугольника и равны их половинам (т.к. являются средними линиями в треугольниках, образованных сторонами и диагоналями).
Диагонали равнобедренной трапеции равны, следовательно стороны параллелограмма Вариньона равны и он является ромбом.
MN - средняя линия в ABC => MN||AC, MN=AC/2. Аналогично LK||AC, LK=AC/2.
MN||LK, MN=LK => MNKL - параллелограмм (противоположные стороны параллельны и равны).
AC=BD, NK=BD/2 => MN=NK => MNKL - ромб (смежные стороны равны).
А(4) и В(10), |4-10|=6
Пошаговое объяснение:
Определим координаты точек A и B:
1) Справа от точки 0 на единичной дальности отмечена число 1, что означает справа от точки 0 направление положительное и цена деления равна 1;
2) точка А отдалена от точки 0 на 4 единицы в положительном направлении, поэтому имеет координату 4, то есть А(4);
3) точка В отдалена от точки 0 на 10 единицы в положительном направлении, поэтому имеет координату 10, то есть В(10).
Расстояние между двумя точками А(x₁) и В(x₂) определяется по формуле AB= |x₁-x₂|. Поэтому расстояние между точками А(4) и В(10) равна |4-10|.
С другой стороны, по рисунку видно, что между точками А(4) и В(10) находится 6 единичных отрезков, поэтому расстояние между точками А(4) и В(10) равно 6.
Тогда |4-10|=6.
Объяснение: