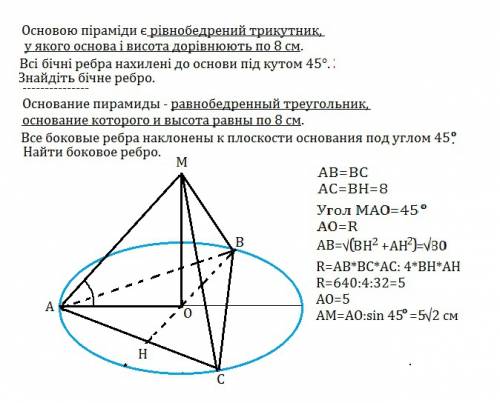
Основою піраміди є рівнобедрений трикутник, у якого основа і висота дорівнюють по 8 см. Всі бічні ребра нахилені до основи під кутом 45°. Знайдіть бічне ребро.
Основание пирамиды - равнобедренный треугольник, основание которого и высота равны по 8 см. Боковые ребра наклонены к плоскости основания под углом 45º. Найти боковое ребро.
Пусть эта пирамида - МАВС.
АВ=ВС, высота ВН основания равна АС=8 см
МО - высота пирамиды.
Ребра пирамиды наклонены под равным углом, следовательно, их проекции равны радиусу описанной вокруг основания окружности. Основание О высоты МО совпадает с центром описанной окружности. Поскольку ребра наклонены под углом 45º, то проекции ребер равны высоте пирамиды МО.
Найдем радиус R описанной окружности.
R=abc/4S, где a,b и c - стороны основания, S - его площадь
Боковые стороны по т.Пифагора:
АВ=√(ВН²+AН²)=√(64+16)=√80
Площадь ∆ АВС=ВН*АС:2=8*8:2=32
R=АВ*АВ*АС: (4*32)=5
В ∆ АОМ ∠ОАМ=45º
АМ=ОА:sin 45=5√2
меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
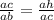
теперь подставим наши значения в эту пропорцию:
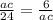
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см

Угол В=55 градусов