Песнь первая:
1) Пир в честь свадьбы Руслана и Людмила.
2) Вещая песнь Баяна, три соперника Руслана.
3) Людмила, похищена безвестной силой.
4) Награда в полцарства и Людмилу, в супруги.
5) Пещера Финна,. судьба похитителя Черномора.
6) История любви старца и Наины.
Песнь вторая:
1) Возвращение Рогдая и встреча с Фарлафом.
2) Предсказание Наины.
3) Людмила в замке Черномора, шапка невидимка.
4) Поединок, гибель Рогдая от руки Руслана.
Песнь третья:
1) Змея-Наина в замке колдуна.
2) Исчезновение Людмилы - невидимки.
3) Бой Руслана с Головой.
4) История брата Черномора.
5) Тайна силы Черномора и волшебный меч.
Песнь четвёртая:
1) Хан Ратмир в замке прекрасной Девы.
2) Руслан на пути к замку колдуна.
3) Коварство Черномора и Людмила в сетях колдуна.
4) Рога звон, Руслан в обители злодея.
Песнь пятая:
1) Битва в облаках.
2) Потеря карлой бороды.
3) Спящая Людмила.
4) Голос Финна и возвращение домой.
5) Вечный сон Головы и рыбак Ратмир.
6) Коварство Наины и убийство Руслана Фарлафом.
Песнь шестая:
1) Возвращение предателя в Киев.
2) Ложь Фарлафа.
3) Воскрешение Руслана вещим Финном, волшебное кольцо.
4) Осада Киева и бегство печенегов от Руслана.
5) Пробуждение Людмилы.
6) Прощение Фарлафа и карлы, конец бедствий и пир
Объяснение:
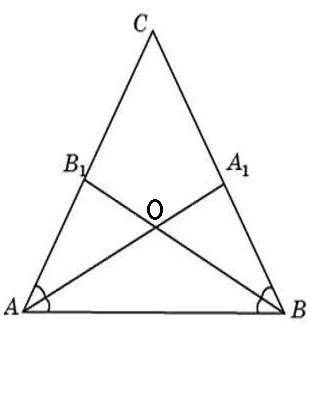
76°
Объяснение:
Признак равнобедренного треугольника: если в треугольнике два угла равны, то такой треугольник - равнобедренный.
1) Рассмотрим ΔАСВ.
∠С =28°, ∠А = ∠В по условию. Т.к. сумма углов 28° Δ-ка равна 180°, то?
∠А + ∠В + ∠С = 180°, откуда
∠А + ∠В = 180° - ∠С = 180° - 28° = 152°. Но ∠А = ∠В по условию, следовательно,
∠А = ∠В = 152°/2 = 76°
2) т.к. ∠А = ∠В , а АА₁ и ВВ₁ - биссектрисы этих углов, то
∠В₁АО = ∠ОАВ = ∠А₁ВО=∠ОВА = 76°/2 = 38°
3) Рассмотрим ΔАОВ.
∠ОАВ = ∠ОВА =38°, тогда
∠АОВ = 180° -2*38° = 180° -76° = 104°
4) ∠АОВ и ∠АОВ₁ - смежные углы, их сумма = 180°, значит,
∠АОВ₁ = 180°-104° = 76°
площадь находим по формуле Герона, для этого находим полупериметр р=1/2(20+20+24)=1/2*64=32 см
S=√(р(р-а)(р-в)(р-с))=√32*12*12*8=√4*8*8*12*12=2*8*12=192
r=S/p=192/32=6 см
2.центр описанной окружности лежит у прям-го тр-ка на середине гипотенузы, поэтому радиус описанной окружности равен половине гипотенузы. Находим ее по теореме Пифагора
с=√(а^2+b^2)=√(36+64)=√100=10
Значит радиус равен 1/2 от 10, т.е. 5 см
3. обозначим сторону равностороннего тр-ка через х. Найдем площадь тр-ка: S=1/2*a*b*sinА=1/2*x^2*√3/2
радиус описанной окружности находим по формуле
R=(a*b*c)/4S, радиус равен 4, из этой формулы находим неизвестное х
4=(x^3)/(4*1/2*x^2*√3/2)=(x^3)/(x^2*√3)=x/√3
Значит х=4*√3