16.
а)
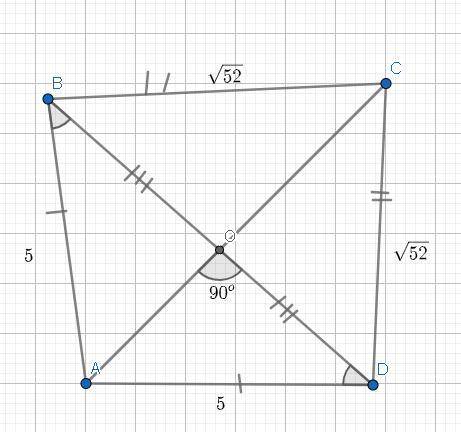
Диагональ BD — делит четырёхугольник на 2 произвольных треугольника: ΔBCD; ΔBAD.
Проведём также диагональ CA: он проходит через ΔBCD.
ΔBCD — равнобёдренный, так как: 
А в свойствах равнобёдренного треугольника входит то, что высота, медиана, и биссектриса, проведённая с вершины к основанию — одно и то же, что и означает, что наш отрезок CO — медиана, и поэтому делит диагональ BD — на 2 равные части.
б)
Я не вижу в этом варианте заданное условие. А если она и вправду есть, то найти площадь, зная то, что отрезки являются "целыми числами", я не смогу.
Но площадь четырёхугольника можно найти — зная всего-лишь его стороны: 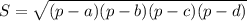
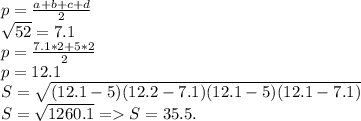
Гипотенуза треугольника лежащего в основании равна 10, по т пифагора Корень из 64+36 сумаа квадратов катетов равна квадрату гипотенузы ну 10 короче. Дальше найдем площадь оснований и сложим их. Площадь основани это площадь треугольника лежащего в основании 1/2*6*8=24 и тк у нас два основания умножаем на 2 т.е 48см^2/
Дальше найдем высоту. Высота тут будет вертикальное ребро тк призма прямая то все три ребра расположены к основанию под углом 90 градусов. Обозначим высоту за х. и теперь мы должны найти сумму площадей трех граней. Тк мы уже нашли площади оснований вычитаем их сумму из площади полной поверхности 288-48=240. теперь запишем сумму площадей граней 6х+8х+10х=240 24х=40 х=10см высота равна 10см.
BC=P(ABCD)/4=36/4=9
∠BAC=∠CAD (AC - биссектриса ∠BAD)
∠BCA=∠CAD (накрест лежащие при BC||AD)
∠BAC=∠BCA => △ABC - равнобедренный, AB=BC
AB=CD, BC=AD (противоположные стороны параллелограмма)
AB=BC=CD=AD => ABCD - ромб.