 делить
делить 
 ,
, 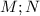 точки касания , тогда и вторая диагональ
точки касания , тогда и вторая диагональ 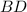 делить
делить 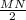 из-за того что трапеция равнобедренная .
из-за того что трапеция равнобедренная . 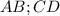 за точки
за точки 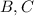 , тогда и замечательного свойства трапеций , того что отрезок соединяющий диагонали и основания , проведенный из вершины проходит через одну точку , но так как трапеция равнобедренная , получим что прямая проведенная с вершины треугольника , будет делить
, тогда и замечательного свойства трапеций , того что отрезок соединяющий диагонали и основания , проведенный из вершины проходит через одну точку , но так как трапеция равнобедренная , получим что прямая проведенная с вершины треугольника , будет делить 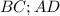 на
на 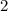 , но так как
, но так как 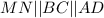 , то и
, то и 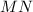 и точки пересечения диагоналей и
и точки пересечения диагоналей и 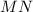 будут пересекаться в одной точке ,а значит изначальное условие было верно .
будут пересекаться в одной точке ,а значит изначальное условие было верно . 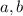 тогда
тогда 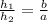
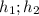 высоты треугольников образованных отрезками диагоналей и основаниями . Получим
высоты треугольников образованных отрезками диагоналей и основаниями . Получим 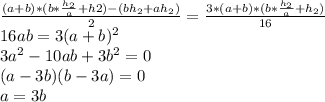
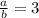
высотой Н=6 см, из которого вырезан конус, радиус основания которого равен 15-7=8 см, высота h=6.
V(тела)=V(цил)-V(кон)=V₁-V₂,
S(пов.тела)=S(пов.цил)-S(осн.кон)+S(бок.кон)=S₁-S(осн.кон)+S(бок.кон) .