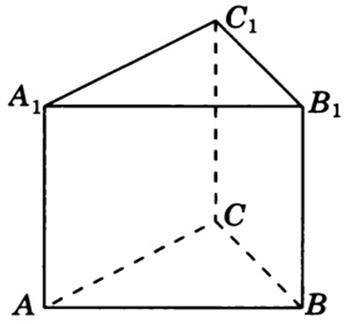
Нехай задана правильна трикутна призма, бічні грані якої є квадратами, а 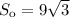 см² — площа основи цієї призми.
см² — площа основи цієї призми.
Основа призми є правильним (рівностороннім) трикутником зі строною  см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника:
см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника: 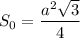
Отже, 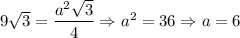 см.
см.
Через те що бічні грані є квадратами, тоді ребра призми дорівнюють 6 см (за властивістю квадрата) — ребра правильної призми є висотою призми.
Об'єм правильної трикутної призми можна розрахувати за формулою
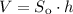 , де
, де 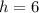 см — висота призми.
см — висота призми.
Знайдено значення шуканої величини:
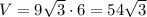 см³
см³
Відповідь: А) 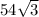 см³
см³
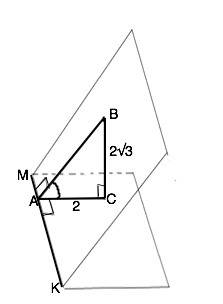
ВС перпендикулярен плоскости, следовательно, перпендикулярен любой прямой, лежащей в этой плоскости и проходящей через его основание С. ⇒ ∆ ВСА - прямоугольный с прямым углом С.
По т.о 3-х перпендикулярах: если наклонная перпендикулярна прямой, лежащей в плоскости, значит, этой прямой перпендикулярна и ее проекция.
ВА - перпендикулярен ребру МК двугранного угла, следовательно его проекция СА перпендикулярна прямой МК.
Величиной двугранного угла является градусная мера его линейного угла.
Линейный угол двугранного угла – угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
АВ и АС перпендикулярны МК. Следовательно, угол ВАC -искомый.
ctg BAC =2:2√3=1/√3 - это котангенс 60°.
Угол ВАС=60°