Есть в данном случае две формулы для вычисления площади ромба
Первая формула.
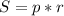, где r - радиус вписанной окружности. p - полупериметр ромба.
В данном случае полупериметр ромба равен 2а, где а - сторона ромба.
Формула принимает вид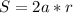 
Найдем радиус круга. Площадь круга равна
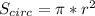
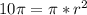
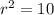
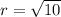
Значит формула приобретает вид
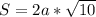
Другая (вторая) формула исходит из формулы параллелограмма
Приравняем правые части формулы
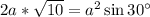
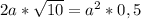
Умножим обе части на 2
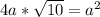
Сократим обе части на а.
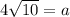
Или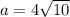 
Подставим в формулу
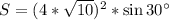
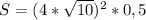
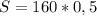
S=80 - площадь ромба
ответ: 80 - квадратных единиц площадь ромба.
Строим трапецию и высоту, точку падения высоты обозначаем как H, тогда AH=4, HD=10.
Аналогично данной высоте проводим высоту из точки C, точку её падения обозначим как M. Тогда AH=MD=4, т.к. треугольники ABH и CMD равны по гипотенузе (боковые стороны трапеции) и катету (высота трапеции).
Нижнее основание AD находится совсем просто: AH+HD=14.
Найдём верхнее основание BC. BC=HM (из прямоугольника BCMH), тогда найдём HM: Если HD=10, а MD=4, то HM=HD-MD=10-4=6. Тогда BC=6.
Средняя линия - полусумма оснований: (BC+AD)/2=10.
в синем треугольнике
гипотенуза в 2 раза длиннее катета против угла в 30°
длинный катет равен половине хорды
По т. Пифагора
d₃² + (а/2)² = (2d₃)²
d₃² + а²/4 = 4d₃²
а²/4 = 3d₃²
d₃² = а²/12
d₃ = а/(2√3)
красный треугольник прямоугольный и равнобедренный, так что
d₄ = а/2
Расстояние меж центрами
d₃ + d₄ = а/(2√3) + а/2 = а/(2√3) + а√3/(2√3) =а(1 + √3)/(2√3) = а(√3 + 3)/6