Даны вершины треугольника А(-2,0,1), В(8,-4,9), С(-1,2,3).
1) Находим длины сторон по разности координат точек.
АВ = √((8-(-2))² + ((-4-0)² + (9-1)²) = √(100 + 16 + 64) = √180 = 6√5.
BC = √((-1-8)² + ((2-(-4))² + (3-9)²) = √(81 + 36 + 36) = √153.
АC = √((-1-(-2))² + ((2-0)² + (3-1)²) = √(1 + 4 + 4) = √9 = 3.
Далее по теореме косинусов определяем углы треугольника.
a(ВС) b(АС) c(АВ) p 2p S
12,36931688 3 13,41640786 14,39286237 28,78572474 18
153 9 180
2,023545494 11,39286237 0,976454506 22,51115808 324 18
cos A = 0,447213595 cos B = 0,97618706 cos С = -0,242535625
Аrad = 1,107148718 Brad = 0,218668946 Сrad = 1,81577499
Аgr = 63,43494882 Bgr = 12,52880771 Сgr = 104,0362435.
Как видим - треугольник тупоугольный.
2) Находим координаты точки М как середины стороны АС.
М = (А(-2,0,1) + С(-1,2,3))/2 = (-1,5; 1; 2).
Длина ВМ = √((-1,5-8)² + ((1-(-4))² + (2-9)²) = √(90,25 + 25 + 49) = √164,25 ≈ 12,81600562.
5
Объяснение:
Чертёж в прикрепленном файле
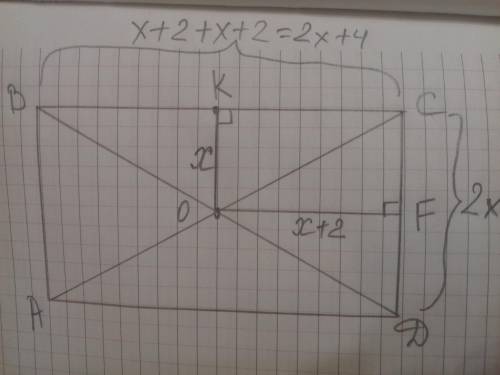
Диагонали прямоугольника равны и точкой пересечения делятся пополам, образуя равнобедренные треугольники. Расстояние от точки О до сторон прямоугольника является высотами в равнобедренных треугольниках, а значит и медианами. Образовавшийся четырехугольник OKCF - прямоугольник, КО=СF= х; КС=OF= х+2,
тогда DA=ВС= ВК+КС = х+2+х+2=2х+4; AB=CD=СF+FD= х + х=2х
Периметр прямоугольника Р=АВ+ВС+СD+DA= 2х+2х+4+2х+2х+4=8х+8
По условию Р=28
8х+8=28
8х=20 разделим обе части на 4
2х=5
т.к. меньшие стороны AB=CD=2х, значит меньшая сторона равна 5.