Пусть АВ=ВС= CD = AD = x, a SM = у — апофема.
Тогда по теореме Пифагора в ∆SMC;
SC2 =SM2 + MC2,
5^2=y^2+x^2/4
то есть х2 + 4у2 = 100.
Полная поверхность равна S = Sосн + Sбок , где Sосн — площадь
квадрата,
Sбок=1/2*P*h
то есть Sосн = х2 и
где P — периметр основания и h — апофема, так что Sбок = 2ху.
Так что х2 + 2ху = 16. Имеем:
x^2+4y^2=100
x^2+2xy=16
y=16-x^2/2x
x^2+4(16-x^2/2x)^2=100 то есть
x4 - 100х2 + (16-х2)2 = 0
х4 - 66х2 + 128 = 0. Пусть х2 = а, тогда
а2 - 66а + 128 =0, а =2 или а = 64. Тогда х = √2 или x = 8.
Но при х = 8 площадь основания больше полной.
Так что х= √2 .
ответ: √2 см.
Надеюсь правильно.
Чертёж смотрите во вложении.
Дано:ΔАВС - прямоугольный.
∠А = 90°.
∠С = 30°.
Точка М - середина СВ.
МН - серединный перпендикуляр.
Доказать:МН < больший катет (АС) в 3 раза.
Доказательство:Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно -
∠С+∠В = 90°
∠В = 90°-∠С
∠В = 90°-30°
∠В = 60°.
Проведём медиану к гипотенузе. Она пересечёт точку М, так как эта точка середина по условию.
Медиана, проведённая к гипотенузе, делит прямоугольный треугольник на два равнобедренных треугольника (так как медиана, проведённая к гипотенузе, равна её половине).
То есть -
ΔАСМ и ΔАМВ - равнобедренные.
Рассмотрим ΔАМВ - равнобедренный. У него есть угол в 60°, а значит, он и равносторонний (признак равностороннего треугольника).
Следовательно, по свойству равностороннего треугольника, ∠АМВ = 60° (каждый угол равностороннего треугольника равен по 60°).
Рассмотрим ΔАСМ - равнобедренный. ∠С = ∠МАС = 30° (так как углы у основания равнобедренного треугольника равны.
Рассмотрим ∠НМВ = 90°.
∠НМВ = ∠НМА+∠АМВ
∠НМА = ∠НМВ-∠АМВ
∠НМА = 90°-60°
∠НМА = 30°.
Так как ∠НМА = ∠НАМ, то ΔАНМ - равнобедренный (по признаку равнобедренного треугольника. Причём НМ = АН (так как лежат против равных углов в одном треугольнике).
Рассмотрим ΔСНМ - прямоугольный. Пусть катет НМ - х.
Против угла в 30° лежит катет, равный половине гипотенузе.
То есть -
СН = 2*НМ
СН = 2х.
Но НМ = АН = х (по выше доказанному).
Поэтому -
АС = СН+АН
АС = 2х+х
АС = 3х.
А теперь составим отношение АС и НМ, и сравним их -
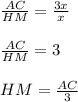
Это нам и нужно было доказать.
ответ:что требовалось доказать.

Выразим через х длины отрезков АС и ВС
1) А(-1;5), х1=-1, у1=5
АС=
2) В(7;-3), х1=7, у1=-3
ВС=
3)
ответ: С(2;0)