Пусть M — середина AB, а N — середина BC. Тогда площадь сечения равна площади треугольника SMN. Найдем последовательно SM, MN иSN.
SM и SN — медианы треугольников SAB и SBC соответственно. Т. к. эти треугольники равносторонние (поскольку все ребра пирамиды одинаковой длины),
.
Найдем теперь MN из прямоугольного треугольника MBN. В нем катеты равны 4. Гипотенуза MN, по теореме Пифагора, будет равна .
Теперь найдем площадь равнобедренного треугольника SMN. Для этого проведем высоту SH, по теореме Пифагора равную , и вычислим площадь:
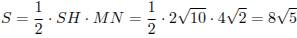
b : √2/2 = 10√2 : 1/2
b = √2/2 * 10√2 : 1/2 = √2 * 10√2 = 10 * 2 = 20.