У трикутнику MNK кут M=44°,а кут N=56°.Бісектриси NE i MP цього трикутника перетинаються в точці O. Установить відповідність між кутами (1-4) утвореного чотирикутника EOPK і кутами , визначеними умовами (А-Д)
1) кут EOP
2) кут OPK
3)кут PKE
4) кут KEO
A. Більший кут рівнобедреного трикутника , у якого менші кути дорівнюють 50°
Б.Кут суміжний з кутом у 50°
В.Менший кут чотирикутника , у якого три кути рівні між собою , а четвертий на 16° менший за кожен з них
Г. Зовнішній кут рівностороннього трикутника
Д. Найменший кут чотирикутника , кути якого пропорційні числам 4,5,5,6.
Ребята

1.
а) Ненулевые векторы t и p называются противоположно направленными, если они лежат либо на одной прямой, либо на параллельных прямых и направлены в противоположные стороны.
б) вектор а равен вектору -b, если длины их равны (|а|=|-b| и вектора противоположно направлены (а⇅b)
в) Векторы с и k*c сонаправлены, если k>0.
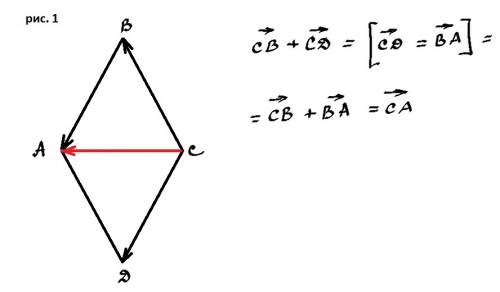
г) Если АВСД ромб, то сумма векторов СВ и СD равна вектору СА (смотри рис. 1)
2.
а) Верно.
б) Неверно, т.к. средняя линия трапеции соединяет середины боковых сторон.
в) Верно.
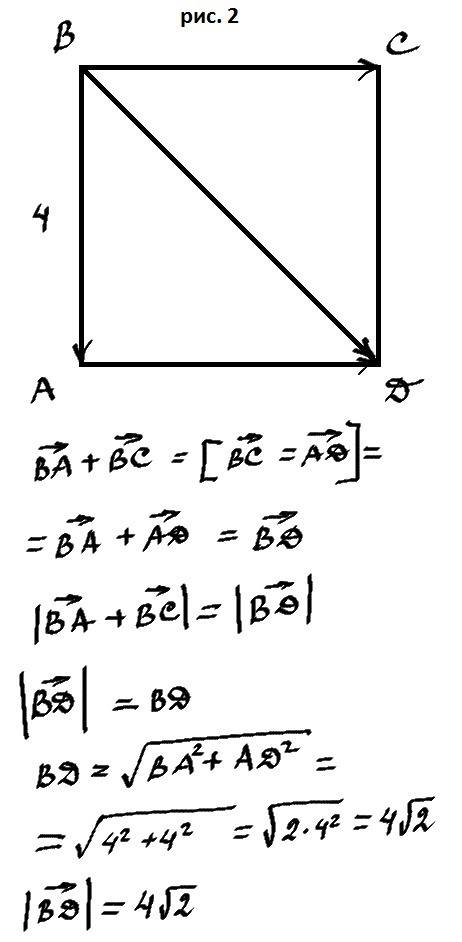
3. б) 4√2 (смотри решение на рис. 2).
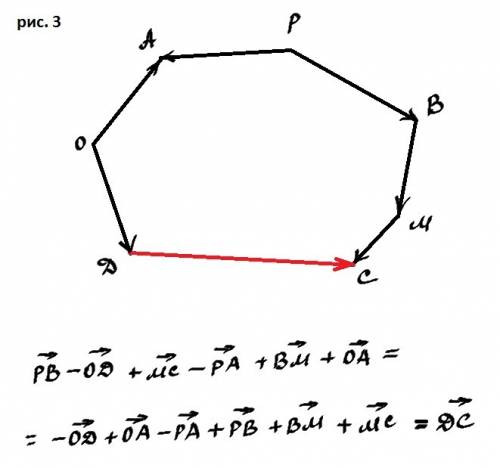
4. в) вектор DС (смотри решение на рис. 3).
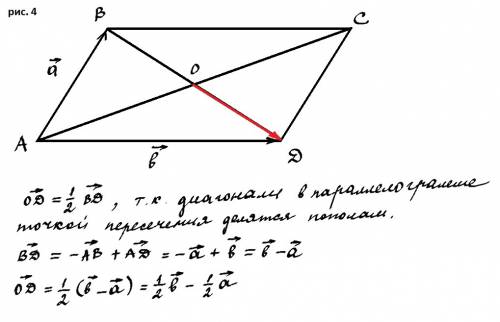
5. Смотри решение на рис. 4.
L = 2πr = 12π
2πr = 12π
r = 6 см
На картинке изображено сечение шара, перпендикулярное основанию шарового сегмента
Из синего прямоугольного треугольника по т. Пифагора
R² = (R-2)² + 6²
R² = R² - 4R + 4 + 36
0 = - 4R + 40
R = 10 см
Площадь шара
S = 4πR² = 4π*100 = 400π см²
---
Объём куба с ребром a = 4 см
V₀ = a³ = 4³ = 64 см³
Объём одного шарика диаметром d = 2 см
V₁ = 4/3*πr³ = 4/3*π(d/2)³ = πd³/6 = π*2³/6 = 8π/6 = 4π/3 см³
Число шаров
N = V₀/V₁ = 64/(4π/3) = 48/π ≈ 15.278
Округляем вниз
N = 15 шт
Объём шарового сегмента при радиусе исходного шара R и высоте сегмента h
V = πh²(R - h/3)
Радиус исходного шара (3+9)/2 = 6 см
Объём меньшего сегмента (h = 3 см)
V₁ = π3²(6 - 3/3) = 9π*5 = 45π см³
Объём большего сегмента (h = 9 см)
V₁ = π9²(6 - 9/3) = 81π*3 = 243π см³