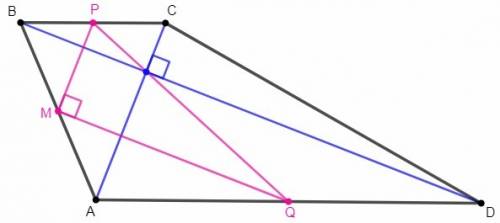
M - середина AB, P - середина BC, Q - середина AD
Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна её половине.
MP - средняя линия в ABC, MP||AC, MP=AC/2
MQ - средняя линия в ABD, MQ||BD, MQ=AD/2
AC⊥BD => MP⊥MQ
По теореме Пифагора
PQ=√(MP^2+MQ^2) =√(AC^2+AD^2)/2 =√194/2
как известно, у параллелограмма противоположные стороны равны. Поэтому, мы можем попробовать составить два вектора - AB и CD
если они параллельны друг другу, то будет выполняться условие AB=CD*n
где n-некое число
AB=(-2-(-5);3-(-6))=(3;9)
CD=(7-10;0-9)=(-3;-9)
Как видно, AB=CD*-1, поэтому вектора AB и CD параллельны
Проверим это же условие для сторон AD и BC
AD=(7-(-5);0-(-6))=(12;6)
BC=(10-(-2);9-3)=(12;6)
Как видно, вектора AD и BC параллельны
Есть еще одно условие: если диагонали четырехугольника пересекаются в одной точке и делятся в ней пополам, то четырехугольник - параллелограмм.
Для этого найдем координаты середин отрезков AC и BD
Как видно, обе диагонали имеют середины в одной и той же точке
Учитывая все доказательства выше, можно говорить, что ABCD - параллелограмм
Длины всех сторон можем найти, посчитав длины векторов выше
AB=(3;9)
CD=(-3;-9)
AD=(12;6)
BC=(12;6)
Объяснение:
Определение-хоронимы: собственное имя любой территории, имеющей определённые границы: небольшого пространства (луг, лес, городской район или микрорайон), исторической области, административного района или страны. Класс топонима.
Примеры:Замоскворечье, Лужники.
Определение-оронимы: собственное название любого объекта рельефа земной поверхности: как выпуклого (гора, горный хребет, холм), так и вогнутого (долина, овраг, впадина, ущелье, котлован), то есть любого орографического объекта; класс топонима
Примеры:гора Эльбрус, Алайская долина, Заалайский хребет, Русские горы, Домбайская поляна, Долгая щель, Боровицкий холм, Воробьёвы горы.
Объяснение: надеюсь
Проведём отрезок СЕ параллельно диагонали ВD => AC перпендикулярен СЕ.
Также проведём отрезок СК параллельно отрезку МN
Из этого следует, что четырёхугольник ВСЕD - параллелограмм ( СЕ || ВD , BC || DE ).
Aналогично, четырёхугольник МСКN - параллелограмм ( CK || MN, МС || KN )
Поэтому, BC = DE , MC = NK, BD = CE = 13
AE = AD + DE = AD + BC
AK = AN + NK = (1/2) × AD + (1/2) × BC = (1/2) × ( ВС + AD )
Значит, K - середина отрезка АЕ , АК = КЕ
Поэтому , МN = CK - медиана в ∆ АСЕ
2) Рассмотрим ∆ АСЕ ( угол АСЕ = 90° ):
" В прямоугольном треугольнике медиана равна половине гипотенузы " →
По теореме Пифагора:
AE² = 13² + 5² = 169 + 25 = 194
AE = √194
Значит, искомый отрезок MN, равный отрезку СК, имеет длину:
СК = MN = (1/2) × AE = (1/2) × √194 = √194/2
ОТВЕТ: √194/2