Объяснение:
Высота равнобедренной трапеции, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
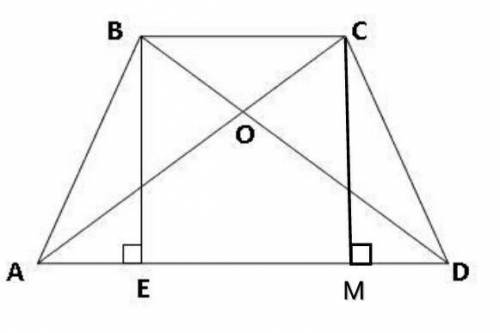
В равнобедренной трапеции АВСD высота ВЕ делит AD на отрезки ЕD=(АD+BC):2 и AE=(AD-BC):2
Подробно:
Если опустить вторую высоту СК, получится прямоугольник ВСКЕ, в котором ЕК=ВС=4. Тогда треугольники АВЕ=КСD по гипотенузе и острому углу (в равнобедренной трапеции углы при основаниях равны). ⇒ АЕ=КD, поэтому каждый из этих отрезков равен половине разности между большим и меньшим основанием. Т.е. АЕ=КD=(AD-BC):2.
Так как в трапеции треугольники ВОС и АОD при основаниях подобны, все неизвестные элементы трапеции можно найти без труда.

a = 4x, b = 5x, c = 7x
P = a + b + c = 4x + 5x + 7x = 16x
16x = 32
x = 32 : 16 = 2 (см)
a = 4*2 = 8 (см)
b = 5*2 = 10 (см)
c = 7*2 = 14 (см)
ответ: 8 см; 10 см; 14 см.