Доказательство
1) Возьмем произвольную точку M на биссектрисе угла BAC, проведем перпендикуляр MK и ML к прямым AB и AC
Рассмотрим прямоугольные треугольники AMK и AML. Они равны по гипотенузе и острому углу. (AM - общая гипотенуза, ∠1∠2 по условию\). Следовательно, MKML
2) Пусть точка M лежит внутри угла BAC и равноудалена от его сторон AB и AC. Докажем, что луч AM - биссектриса угла BAC
Проведем перпендикуляры MK и ML к прямым AB и AC. Прямоугольные треугольники AMK и AML - равны по гипотенузе и катету (AM - общая гипотенуза, MKML по условию ). Следовательно, ∠1∠2. Но это и значит, что луч AM - биссектриса угла BAC. Теорема доказана
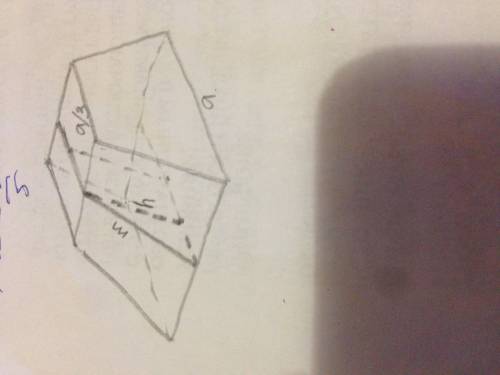
Второй угол треугольника в основании (90 - альфа).
Теперь главное - ясно, что вершина пирамиды проецируется в центр вписаной окружности. Это потому, что основание высоты равноудалено от сторон на расстояния, равные высоте пирамиды, умноженной на ctg(бета). Если аккуратно построить двугранные углы боковых граней, опуская перпендикуляры на стороны основания, то это сразу видно.
Центр вписаной окружности лежит на пересечении биссектрис. Поэтому
r = b*sin(альфа/2);
Боковые стороны тоже легко вычисляются, один катет = r + b*cos(альфа/2);
второй = r+ r*ctg(45 - альфа/2).
Высота пирамиды равна r*tg(бета). Отсюда всё находится.
S = (1/2)*(b^2)*(sin(альфа/2) + cos(альфа/2))*sin(альфа/2)*(1+ctg(45 - альфа/2));
Наверно, это выражение можно упростить. Мне удалось до такого выражения:
S = (b^2/2)*(1 + sin(альфа) - cos(альфа))*(1+sin(альфа)+cos(альфа))/(2*cos(альфа))
Надеюсь, я нигде не ошибся. На всякий добавил скан, как я упрощал.
V = (1/3)*S*b*sin(альфа/2)*tg(бета)