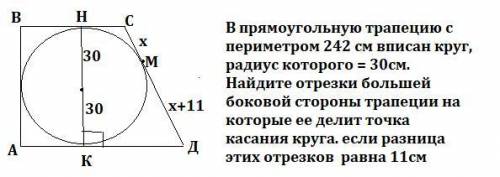
В прямоугольную трапецию с периметром 242 см вписан круг, радиус которого = 30см. Найдите отрезки большей боковой стороны трапеции на которые ее делит точка касания круга. если разница этих отрезков равна 11см
Объяснение:
Большая боковая сторона это СД
Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны⇒АВ+СД=ВС+АД=242:2=121 (см).
Радиус, проведенный в точку касания перпендикулярен касательной ⇒ R=НК=АВ=30*2=60(см).
Значит АВ+СД=121 , 60+СД=121 , СД=61 см.
Пусть меньший отрезок стороны СД будет х см, тогда больший отрезок стороны СД= будет х+11, а из сумма 61 см. Составим уравнение : х+х+11=61 , х=25см
Меньший отрезок 25 см, больший отрезок 25+11=36 (см)
Назовем серединный перпендикуляр к стороне ВС-ОН. Треугольник НОВ=треугольнику НОС (по двум сторонам и углу между ними) ВН=НС (т. к. ОН-серединный перпендикуляр) , сторона ОН-общая, угол ОНВ=углу ОНС=90 (т. к ОН-перпендикуляр) . Тогда ВО=ОС=10. Расстоянием от точки О до АС-будет являться серединный перпендикуляр ОН1. Треугольник СН1 О-прямоугольный (СН1-перпендикуляр) , угол ОСН1=30 (это тот же угол АСО) . В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы, тогда ОН1=0,5 ОС=0,5*10=5
Объяснение:
Правильный ответ на вопрос «В треугольнике abc серединные перпендикуляры к сторонам AB и BC пересекаются в точке O, BO=10 см, угол ACO=30 градусов. Найдите расстояние ...» по предмету Геометрия
Если в треугольнике АВС: BE=EC и AK=KC, то отрезок КЕ - средняя линия треугольника и равна 0,5 стороны АВ. А так как ВС=2*ЕС и АС=2*КС (дано), то периметр треугольника АВС равен Pekc*2=15,5*2 = 31 см.
ответ: Pabc=31см.