прямоугольный треугольник
В решении задачи пригодится
1)Теорема о трех перпендикулярах.
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна этой наклонной.
2) Теорема Пифагора.
Решение.
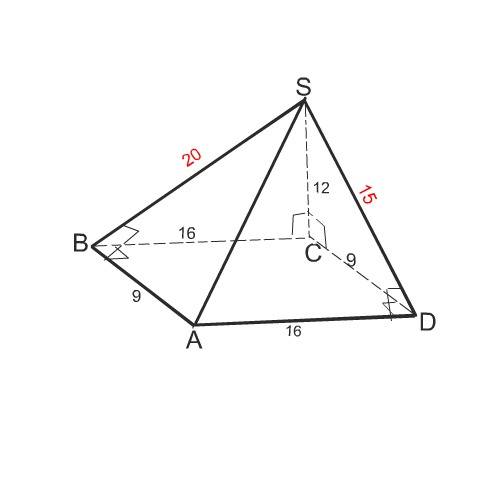
Основание АВСD пирамиды SАBСD- прямоугольник.
Наклонные SB и SD имеют проекции ВС и CD
Прямая ВА перпендикулярна проекции ВС наклонной SB.
АВ перпендкулярна SB.
Прямая АD перпендикулярна проекции СD наклонной SD.
АD перпендикулярна SD
Углы SDА и SВА - прямые.
Следовательно, Δ SDА и ΔSВА - прямоугольные.
SС перпендикулярна плоскости основания, ⇒ перпендикулярна ВС и СD.
Δ SСB и ΔSСD - прямоугольные.
Все грани пирамиды пирамиды SАBСD - прямоугольные треугольники.
Площадь прямоугольного треугольника равна половине произведения его катетов.
Катеты треугольников SСB и SСD даны в условии задачи.
Это SС и СB в треугольнике SСB,
Это SС и СD в треугольнике SСD.
Катеты треугольника SВА - сторона ВС основания и
гипотенуза SВ треугольника SСB
Катеты треугольника SDА - сторона СD основания и
гипотенуза SD треугольника SСD.
Найдем SВ и SD по теореме Пифагора.
SD =√(СD² +SС²)=√(9²+12²)=15 см
SВ =√(SС²+ВС²)=√(16²+12²)=20 см
Площадь боковой поверхности пирамиды равна сумме площадей боковых граней пирамиды.
Площадь Δ SCВ =СS·BC:2=12·16:2
-"-"-"-"-"-"- Δ SВА=SВ·ВА:2=20·9:2
-"-"-"-"-"-"- Δ SDА=SD·DА:2=15·16:2
-"-"-"-"-"-"- Δ SСD=SC·СD:2=12·9:2
S боковая=(12·16+20·9+15·16+12·9):2
S боковая=(192+ 180+ 240+108):2=360 см²
№1
S1=8*8=64
S2=15*15=225
S3=225+64=289
сторона третьего квадрата =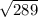 
= 17см.
№2.
Е
В О С
А Д
Что бы доказать, что площадь прямоугольника ABCД равна площади треугольника AEД, надо доказать, что площадь треугольника ЕВО=площади треугольникаОСД (т.е. треугольники равны), т.к. пдощадь АВСД=площадьАВОД+площадьОСД.
АВ=ВЕ (по построению)
АВ=СД (по св-вам прямоугольника)
следовательно ВЕ=СД
уголОЕВ=углуСДО (т.к. накрест лежащие для АЕ II СД и секущей ЕД)
угол ОСД=углуЕВО=90градусов
следовательно тр.ВЕО=тр.ОСД по стороне и двум прилежащим углам (по II признаку)
Что и требовалось доказать.
ответ в, попробуй начерти его