Вся хитрость в том, что отсекаемый биссектрисой треугольник (от параллелограмма) обязательно равнобедренный. Углы при его основании равны, поскольку один из них - внутренний накрест лежащий при параллельных сторонах и биссектрисе (как секущей) с одним из углов, на которые биссектриса делит угол параллелограмма.
Ясно, что одна сторона 21, а вторая может быть либо 7, либо 14, в зависимости от того, от какой вершины отсчитываются отрезки 7 и 14 :) Поэтому и ответа два, периметр может быть 56 или 70.
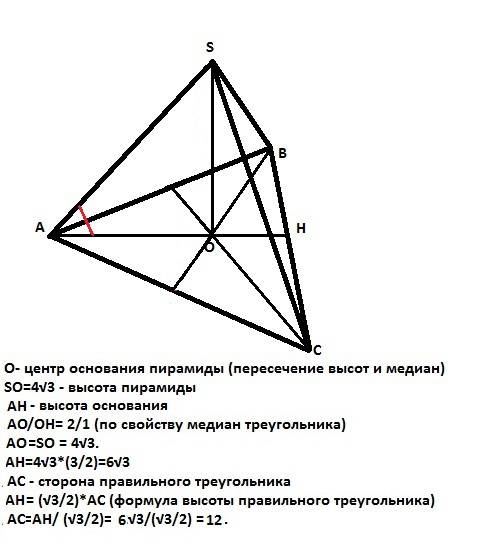
ав и ас - наклонные, ов=8 см(проекция ав на плоскость альфа), ав = 10 см,
проведем с пункта а перпендикуляр к плоскости, пункт пересечения обозначим о.
треугольник аво - прямоугольный( ао - перпендикуляр)
найдем ао по теореме пифагора:
ао^2 = 10^2 - 8^2
ao^2 = 36
ao = 6
треугольник сао - прямоугольный( ао - перпендикуляр)
са = 2ао = 2*6=12 см( гипотенуза в два раза больше катета, которай лежит напротив угла в 30 градусов)
ответ: 12 см