Пусть дано ΔАВС i ΔА 1 В 1 С 1 причем АС = А 1 С 1 , ВМ i B 1 M 1 - медианы, ВМ = B 1 M 1 , ∟BMC = ∟B 1 M 1 C 1 .
Докажем, что ΔАВС = Δ А 1 В 1 С 1 .
Рассмотрим ΔВМС i ΔB 1 M 1 C 1 .
1) ВМ = B 1 M 1 (по условию)
2) ∟BMC = ∟В 1 М 1 С 1 (по условию)
3) МС = М 1 С 1 (половины равных стopiн AC i A 1 С 1 ).
Итак, ΔВМС = ΔВ1М1С1 за I признаку.
Рассмотрим ΔАВС i Δ А 1 В 1 С 1 .
1) AC = А 1 С 1 (по условию)
2) ∟C = ∟C 1 (т. К. ΔВМС = Δ B 1 M 1 C 1 )
3) ВС = В 1 С 1 (т. К. ΔВМС = Δ B 1 M 1 C 1 ).
Итак, ΔАВС = ΔА 1 В 1 С 1 , за I признаку.
Объяснение:
Дано:
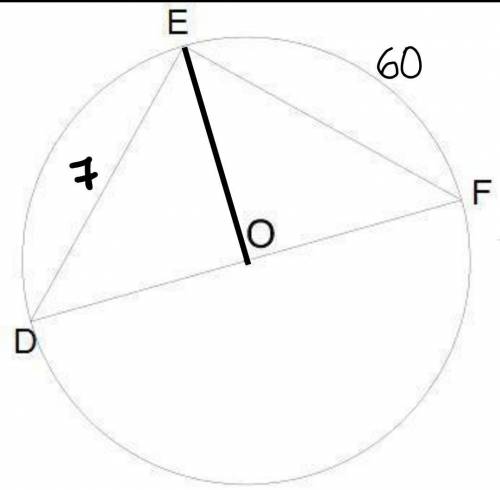
Окружность с центром в точке О;
Дуга ED=60°;
ED=7 см.
Найти: длину окружности.
Проведем ЕО.
Угол ЕОF – центральный и опирается на дугу EF, тогда угол EOF=дуга EF=60°.
Угол DOE=180°–угол EOF=180°–60°=120° (смежные углы)
DO=EO так как радиусы равны, следовательно ∆ЕОD – равнобедренный с основанием ED.
Углы при основании равнобедренного треугольника равны, тогда угол DEO=угол ODE=(180°–угол DOE)÷2=(180°–120°)÷2=60°÷2=30°.
По теореме синусов в ∆EOD:
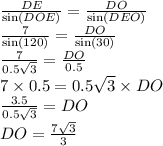
DO – радиус окружности.
C=2πr, где С – длина окружности; r – радиус окружности.
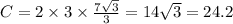
ответ: 24,2 см.
1) 8-6=2-В
2)16-6 = 10 А
3)2+10= 12-АВ