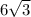ответ: 95,04
Объяснение: при проведении высоты образуются два прямоугольных треугольника с катетами равными высотой и половине основания равнобедренного треугольника, гипотенузой является боковая сторона равнобедренного треугольника. Для того, чтобы найти высоту равнобедренного треугольника, нужно боковую сторону умножить на синус угла и получим: h=15*0,48=7,2
Длина основания будет равна удвоенному произведению боковой стороны на косинус острого угла.
cos=√1-sin²=√1-0,48²=√0,77=0,88
Основание равно: 15*0,88*2=26,4
Площадь равнобедренного треугольника равна: 26,4*7,2/2=95,04
20° и 70°
Объяснение:
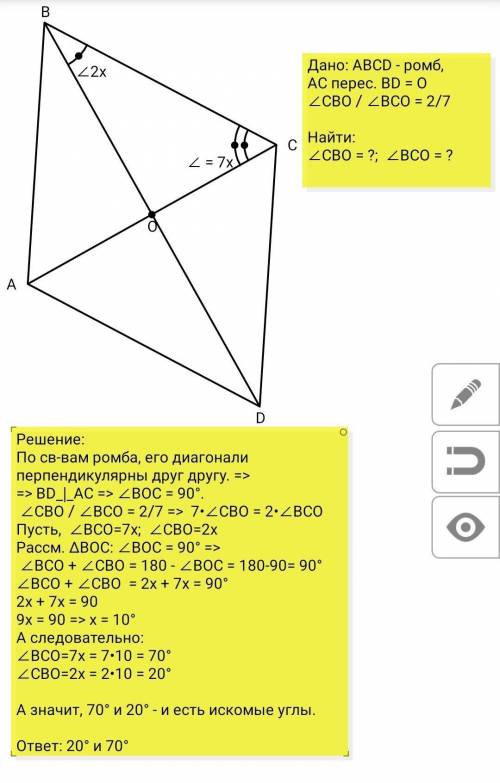
См. на приложенном рис.
Дано:
АВСD - ромб,
АС перес. ВD = O
∠CВO / ∠BСO = 2/7
Найти:
∠CBO = ?; ∠BCO = ?
По св-вам ромба, его диагонали перпендикулярны друг другу. =>
=> ВD_|_AC => ∠BOC = 90°.
∠СВО / ∠ВСО = 2/7 => 7•∠СВО = 2•∠ВСО
Пусть, ∠ВСО=7х; ∠СВО=2х
Рассм. ∆ВОС: ∠ВОС = 90° =>
∠ВСО + ∠СВО = 180 - ∠ВОС = 180-90= 90°
∠ВСО + ∠СВО = 2х + 7х = 90°
2х + 7х = 90
9х = 90 => х = 10°
А следовательно:
∠ВСО=7х = 7•10 = 70°
∠СВО=2х = 2•10 = 20°
А значит, 70° и 20° - и есть искомые углы.
ответ: 20° и 70°
Проведем от точки В к плоскости α перпендикуляр ( назовем эту точку О)
у нас получился прямоугольный треугольник АВ с гипотенузой АВ=12 и углом =60°
мы можем найти угол АВО = 90-60=30°(по св. прям. тр.)
По другому свойству мы можем найти АО( катет, напротив которого угол в 30°)
АО равняется половине гипотенузе, а значит 6 см
По теореме Пифагора находим расстояние от точки В до плоскости (или ВО):
ВО²=АВ²-АО²
ВО²=144-36=108
ВО=
ответ: