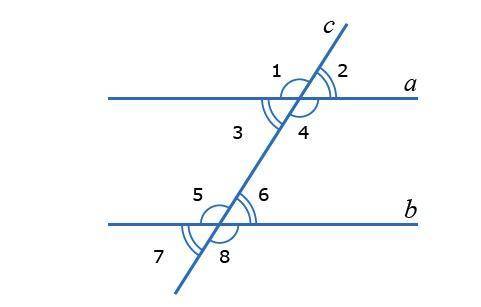
∠2=∠3=∠6=∠7=65°
∠1=∠4=∠5=∠8=115°
Объяснение:
∠1 и ∠2 - смежные углы. Их сумма равна 180°
Пусть ∠2=х°, тогда ∠1=(х+50)°, их сумма 180°:
х+х+50=180
2х=130
х=65°
∠2=65°, ∠1=115°
∠3=∠2 - как вертикальные углы. ⇒∠3=65°
∠6=∠3 - как внутренние накрест лежащие углы при параллельных прямых а и b и секущей с. ⇒ ∠6 = 65°
∠7=∠6 - как вертикальные углы ⇒ ∠7=65°
∠4=∠1 - как вертикальные углы. ⇒∠4=115°
∠5=∠4 - как внутренние накрест лежащие углы при параллельных прямых а и b и секущей с. ⇒ ∠5 = 115°
∠8=∠5 - как вертикальные углы ⇒ ∠8=115°
Т.к. АВСД - ромб, то у него все стороны равны, диагонали пересекаются под прямым углом и в точке пересечения делятся по-полам. АО=ОС; ВО=ОД=3см (6/2).
Прямая ОК перпендикулярна плоскости, значит и перпендикулярна всем прямым на этой плоскости. ОК перпендикулярна прямым ВД и АС.
Рассмотрим треугольник АОВ - прямоугольный. По теореме Пифагора
АО= sqrt(АВ^2- ВО^2)=sqrt(25-9)=4см
Опускаем наклонные из точки К к прямым АО и ВО.
Из треугольника АОК- прямоугольного по теореме Пифагора АК=sqrt(64+16)=sqrt(80)= 4sqrt(5)/
Из треугольника ВКО - прямоугольного, ВК= sqrt(64+9)=sqrt(73) см
ОТВЕТ:sqrt(80); sqrt(73).
5, 12 и 13 - пифагоровы числа, 25 + 144 = 169; АВС - прямоугольный треугольник.
поэтому АС перпендикулярен СВ,
и АС перпендикулярен ВD (по условию)
поэтому АС перпендикулярен плоскости ВСD, а значит, и прямой CD