Стороны данного треугольника равны 15 см, 20 см, 30 см. Найдите стороны треугольника с периметром 26 см, подобного данному треугольнику. Покажите, что отношение площадей треугольников ABC и A1B1C1 равно (3)
Объяснение:
Т.к. стороны ΔАВС равны 15 см, 20 см, 30 см , то отношение этих сторон 3:4:6. Такое же отношение сторон будет и в подобном ΔА₁В₁С₁.
Пусть одна часть сторон ΔА₁В₁С₁ будет х , тогда длина сторон будет равна 3х, 4х,6х.
Т.к. Р(А₁В₁С₁) =26 см , то 3х+ 4х +6х =26 , х=2.
Тогда стороны ΔА₁В₁С₁ такие 6 см ,8 см ,12 см.
Найдем коэффициент подобия к=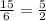 
.
По т. об отношении площадей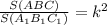 
,получаем
.
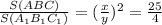А 3 не получается.
трапеция АВСД, АВ=СД, уголА=уголД, АС=2*корень5, СН-высота на АД=2, диагонали в равнобокой трапеции равны , АС=ВД=2*корень5, из точки С проводим линию параллельную ВД до пересечения ее с продолжением АД в точке К,
ДВСК параллелограмм, ВС=ДК, СК=ВД=2*корень5, треугольник АСК равнобедренный, СН-высота=медиане, АН=НК=1/2АК, треугольник АСН прямоугольный, АН=корень(АС в квадрате-СН в квадрате)=корень(20-4)=4, АК=АН*2=4*2=8,
площадь АСК=1/2*АК*СН=1/2*8*2=8=площадь трапеции АВСД (площадь трапеции=1/2*(ВС(ДК)+АД)*СН, но ДК+АД=АК, тогда площадь=1/2*АК*СН)
В равнобедренном треугольнике АВС углы А и С при основании равны, а сумма трех внутренних углов равна 180°. Отсюда следует, что 2*<A+2*<A - 10° =180° и 2*<A = 95°. Тогда третий (больший) угол равен 95-10=85° Это ответ.