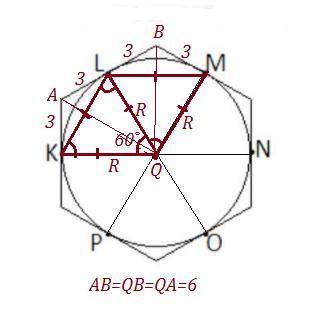
Шестиугольник правильный => у него все углы равны. Из свойств правильного шестиугольника: сторона равна радиусу описанной окружности a=R=6 см; каждый угол правильного шестиугольника равен 120°. Мысленно построив точку О и проведя из вершин шестиугольника отрезки мы получим 6 одинаковых равносторонних треугольников с углами 60°.
Для нахождения радиуса вписанной окружности используем формулу:
r = R cos 180/n
где n - количество сторон.
r = 6 cos 30 = 3√3
Находим длину вписанной окружности:
2Пr = 6П√3
Из рисунка очевидно, что требуемая длина дуги KLM составляет ровно 1/3 от общей дуги, тогда:
KLM = 6П√3 : 3 = 2П√3
Объяснение:
ВС=6 см биссектриса АС делит угол ВАD пополам, т.е. ВАС=CAD (1=2 на рисунке). ВС параллельна AD, то угол ВСА будет равен CAD. Отсюда получается, что треугольник АВС равносторонний и АВ в нем равна ВС, т.е. те же 6 см.
P.S. простите, школу закончил в 1998, не помню, как называется теорема, когда параллельные прямые пересекает отрезок и при этом противоположные углы равны. В нашем случае это ВСА и САD