а) AM= 6, BM=9
б) r=4,5
Объяснение:
Для того чтобы не запутаться: n-BC, d-AC, m-AB.
Это на каких сторонах находятся точки.
1. Найдем третью сторону треугольника:
P=a+b+c
bc=48-(15+15)=18
2. Поскольку треугольник равнобедренный, точка касания, делит сторону BС на два равных отрезка:
BN=NC=9
3. По свойству касательных к окружности:
BN=NC=9
AM=AB-BM
(BM будет равно BN)
AM=15-9=6
4. Радиум можно будет найти по формуле площади:
r=
(p-полупериметр)
S=
Ну или же:

(AD-высота, ее можно найти по теореме Пифагора: AD=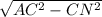 ; AD=
; AD=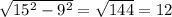 )
)
S=12*9=108
p=48:2=24
r=108:24=4,5
В прямоугольном треугольнике ABC СМ - медиана, проведенная к гипотенузе AB. Найдите величину большего острого угла треугольника АВС, если угол АМС равен 124°.
ответ: 62°
Объяснение:
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине:
АМ = СМ = ВМ.
ΔАМС равнобедренный, углы при основании равны:
∠МАС = ∠МСА = (180° - 124°) / 2 = 28°.
Сумма острых углов прямоугольного треугольника равна 90°, значит
∠В = 90° - ∠МАС = 90° - 28° = 62° - больший острый угол.