МК-средняя линия, следовательно МК=АВ:2=4см; МС=4,5; КС=5, Рмкс=4+4,5+5=13,5 (см)
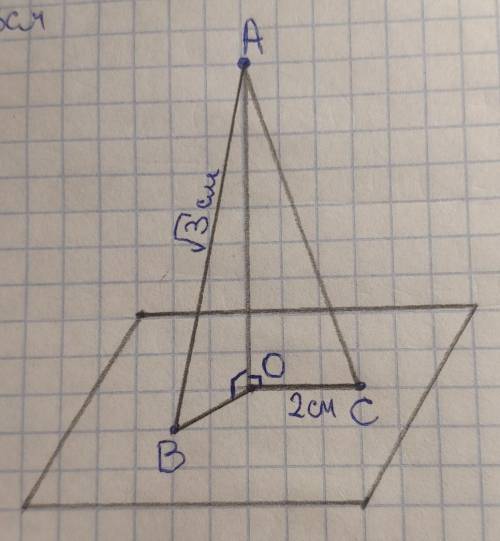
Прямая, перпендикулярная плоскости, перпендикулярна всем прямым, лежащим на этой плоскости.
Следовательно угол АОВ=угол АОС=90°, значит ∆АОВ и ∆АОС – прямоугольные.
ВО+АС=3 см по условию. Пусть ВО=х, тогда АС=3–х.
В прямоугольном ∆АОВ по теореме Пифагора:
АВ²=АО²+ВО²
(√3)²=АО²+х²
АО²=3–х² (Ур 1)
По теореме Пифагора в прямоугольном ∆АОС:
АС²=ОС²+АО²
(3–х)²=2²+АО²
АО²=9–6х+х²–4
АО²=х²–6х+5 (Ур 2)
Подставим значение АО² из уравнения 1 в уравнение 2, получим:
3–х²=х²–6х+5
2х²–6х+2=0
х²–3х+1=0
Д=(–3)²–4*1*1=9–4=5
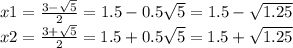
Тогда ВО=1,5+√1,25 или ВО=1,5–√1,25
Катет прямоугольного треугольника всегда меньше гипотенузы, то есть ВО<АВ
1,5+√1,25<√3
1,5+1,118<1,732
2,618<1,732
Неверно
1,5–√1,25<√3
1,5–1,118<1,732
0,382<1,732
Верно, следовательно ВО=1,5–√1,25 см.
Тогда АС=3–(1,5–√1,25)=3–1,5+√1,25=1,5+√1,25
ответ: ВО=1,5–√1,25 см, АС=1,5+√1,25 см.
ответ: arctg(√2tgα).
Объяснение:"Углом между указанными плоскостями MDC и АВС является угол, стороны которого – лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру".
1) ΔДОС: ОД=ОС по свойству диагоналей квадрата,
ОЕ- медиана по условию ⇒ОЕ- высота и ∠ОЕС=90°.
2) ΔОЕС: ∠ОЕС=90°, пусть ДС=а, тогда ОЕ=ЕС=а/2,
ОС²=(а/2)²+(а/2)²=а²/4 + а²/4= 2а²/4= а²/2;
ОC=а:√2= (а√2) :2.
ОМ:ОС=tgα ⇒ ОМ=ОС*tgα= (а√2) :2 * tgα= (а√2*tgα) :2.
3) ΔОМЕ: ОМ⊥ пл.АВС, ОЕ⊂пл.АВС ⇒ ОМ⊥ОЕ.
tg∠ОЕМ = ОМ:ОЕ = (а√2*tgα):2 :а/2= (а√2*tgα):а= √2tgα;
4) ОЕ⊂пл.АВС, ОЕ⊥ДС, МЕ- наклонная к пл.АВС,
ОЕ- проекция МЕ на пл.АВС ⇒
⇒ по теореме о трёх перпендикулярах МЕ ⊥ ДС.
пл.АВС ∩ пл.ДМС= ДС, МЕ ⊂ пл.ДМС и МЕ⊥ДС,
ОЕ ⊂ пл.АВС и ОЕ⊥пл. АВС ,
значит ∠(МДС;АВС)=∠ОЕМ= arctg(√2tgα).
Решение
1)т.к МK-средняя линия из этого следует что
МК=половине АВ
МК=4 см
2) т.к МК-средняя линия точка М делит сторону пополам СВ и точка К тоже делит сторону пополам АС. из этого следует что точка
МС = половине ВС
МС=4.5 см
КС=половине АС
КС= 5 см
P=4.5 см + 4 см + 5= 13.5 см