Окружность с центром О.
ВС - диаметр.
А ∈ окружности с центром О.
∠АОС = 35°
Найти:∠ВАО - ?
Решение:
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
⇒ ∠ВАО + ∠ОВА = 35° (∠АОС = 35°, по условию)
Так как ∠ОВА = ∠ВАО, по свойству ⇒ ∠ОВА = ∠ВАО = 35°/2 = 17,5°
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Сумма смежных углов равна 180°.
∠АОС смежный с ∠ВОА ⇒ ∠ВОА = 180° - 35° = 145°
Сумма углов треугольника равна 180°.
⇒ ∠ВАО = ∠ОВА = (180° - 145°)/2 = 17,5°
ответ: 17,5°.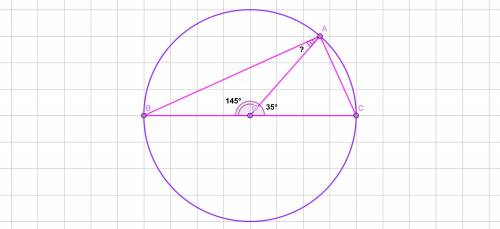
Окружность с центром О.
ВС - диаметр.
А ∈ окружности с центром О.
∠АОС = 35°
Найти:∠ВАО - ?
Решение:
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
⇒ ∠ВАО + ∠ОВА = 35° (∠АОС = 35°, по условию)
Так как ∠ОВА = ∠ВАО, по свойству ⇒ ∠ОВА = ∠ВАО = 35°/2 = 17,5°
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Сумма смежных углов равна 180°.
∠АОС смежный с ∠ВОА ⇒ ∠ВОА = 180° - 35° = 145°
Сумма углов треугольника равна 180°.
⇒ ∠ВАО = ∠ОВА = (180° - 145°)/2 = 17,5°
ответ: 17,5°.
Основная теорема, на которой базируется решение практически всех задач, звучит так: высота в равнобедренном треугольнике является биссектрисой и медианой.
Докажем , что биссектриса в равнобедренном треугольнике- это высота и медиана:
1) Биссектриса делит треугольник пополам .
2) Высота равнобедренного треугольника-это линия проведённая из вершины до противоположной стороны.
Вывод: Что биссектриса , что высота, что медиана равнобедренного треугольника являются равными и образуют 2 прямых угла при основании.