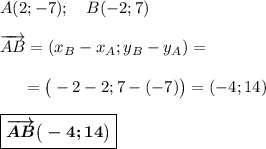
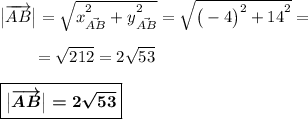
В трапеции ABCD биссектриса угла BAD проходит через точку М, которая является серединой CD. Известно, что АВ=5, АМ=4. Найдите длину отрезка ВМ.
По условию СМ=CD.
Решить задачу можно разными
Проведем МК || AD - по т. Фалеса она делит АВ в отношении DM:MC т.е. на АК=КВ.
В ∆ АКМ ∠КМА= ∠МАD - как накрестлежащие.
∠МАD=∠МАК- как половины ∠КАD
∠КАМ=∠КМА⇒
∆ АКМ - равнобедренный, и АК=КМ.
Но КМ=АК=КВ ⇒ ∆ ВКМ равнобедренный, ⇒ ∠КВМ=∠КМВ.
Углу КМВ равен накрестлежащий ∠ СВМ. ⇒ ВМ - биссектриса угла СВК.
В трапеции сумма углов, прилежащих к одной боковой стороне, равна 180º
Тогда сумма их половин равна 90º, и угол ВМА=180º-90º=90º
∆ АВМ - прямоугольный. Отношение катета АМ к гипотенузе АВ 3:5⇒ ∆ АВМ - египетский, и ВМ=3 (ед. длины) ( по т.Пифагора получим ту же величину).
Доказав, что ∆ АКМ - равнобедренный, проведем в нем высоту КН. Она же - медиана, и АН=НМ.
Тогда КН - средняя линия ∆ АВМ, и КН || ВМ, откуда следует, что угол ВМА=90º, ∆ АВМ - египетский и ВМ=3 (ед. длины).
на любителей т. косинусов)
По т. косинусов можно из ∆ КАМ найти косинус угла КАМ, затем по ней той же теореме длину ВМ.
Вычисления приводить не буду - пользовалась при нахождении косинуса инженерным калькулятором. Без него значения будут лишь приближенными. Таким образом найден
cos ∠КАМ=0,8.
Тогда ВМ²=5²+4²-2•5•4•0,8 ⇒
BM²=25+16-32=9
BM=3 (ед. длины)

