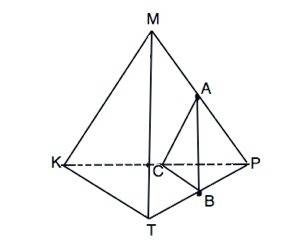
По условию секущая плоскость параллельна плоскости КМТ.
Точки А и В лежат в плоскости грани МРТ и являются серединами сторон МР и ТР треугольника МТР.
Следваоетльно, прямая АВ параллельна МТ.
Из т.В проведем прямую ВС параллельно КТ.
ВС - средняя линия ∆ КТР.
С- середина КР, АС - средняя линия ∆ МКР и параллельна МК.
Две пересекающиеся прямые АВ и МС плоскости АВС параллельны двум пересекающимся прямым МТ и ТК плоскости МКТ. Это признак параллельности плоскостей, следовательно, АВС - искомое сечение.
1. Уравнение прямой имеет вид ах+bу+с=о .
у-у1= (у2-у1)\(х2-х1)*(х-х1)
у-(-1)=(2-(-1))\(8-(-3))*(х-(-3))
у+1=(2+1)\(8+3)*(х+3)
у+1=3\11*(х+3)
у=(3х+9)\11-1
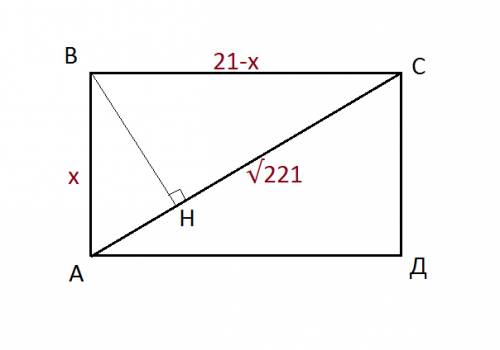
2. Пусть х1 и у1 - координаты точки С,а х2 и у2 - координаты точки D, найдем длину CD:
Смотри картинку
Получим уравнение окружности:
Смотри картинку